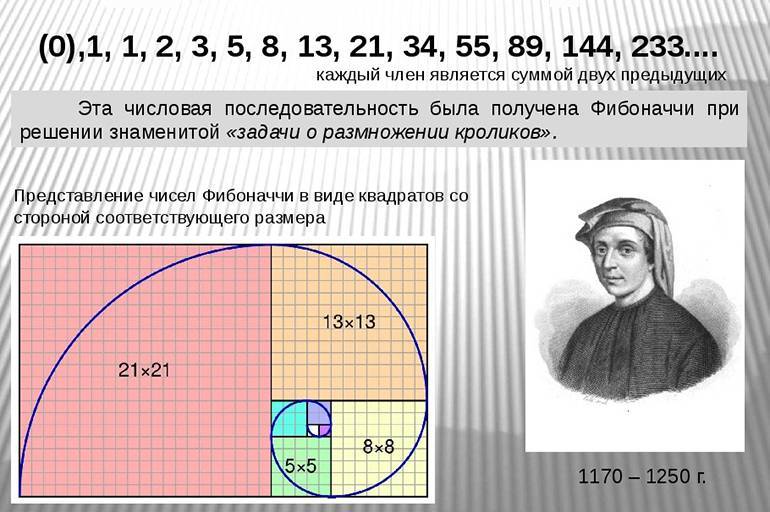
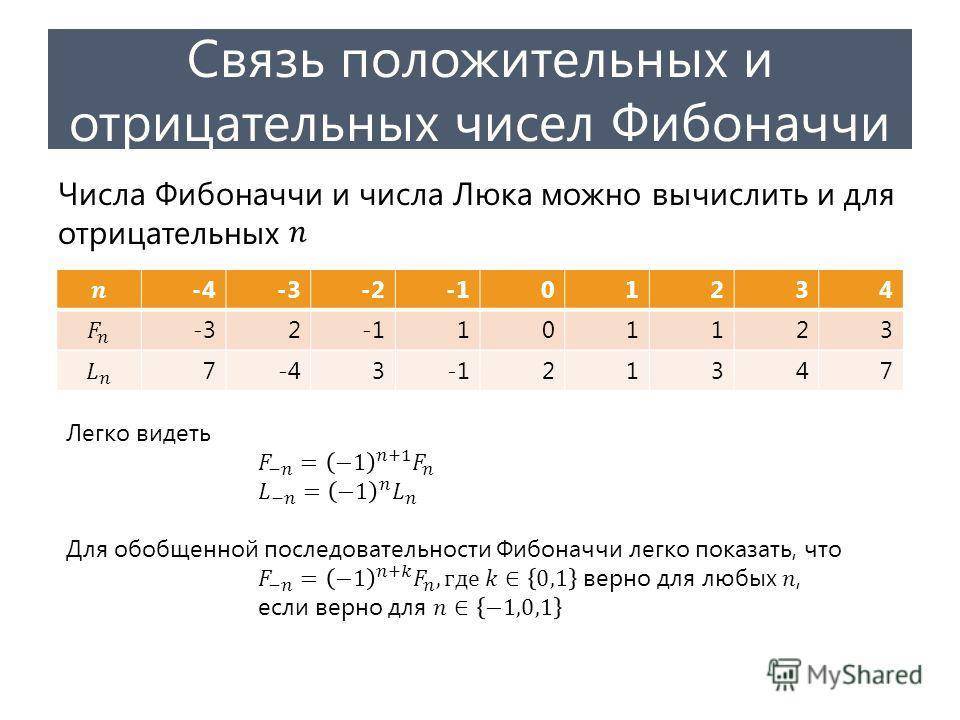
Введение
Программистам числа Фибоначчи должны уже поднадоесть. Примеры их вычисления используются везде. Всё от того, что эти числа предоставляют простейший пример рекурсии. А ещё они являются хорошим примером динамического программирования. Но надо ли вычислять их так в реальном проекте? Не надо. Ни рекурсия, ни динамическое программирование не являются идеальными вариантами. И не замкнутая формула, использующая числа с плавающей запятой. Сейчас я расскажу, как правильно. Но сначала пройдёмся по всем известным вариантам решения.
Код предназначен для Python 3, хотя должен идти и на Python 2.
Для начала – напомню определение:
Fn= Fn-1+ Fn-2
и F1= F2=1.
Где в МетаТрейдере находятся инструменты ряда чисел Фибоначчи
Чтобы увидеть на графике фибо-разметку, надо зайти в меню «Вставка» (выделено голубым контуром на рис. 4) указать на пункт «Фибоначчи» и кликнуть на требуемом варианте. Всего встроено по умолчанию в MetaTrader 5 инструментов:
- Линии;
- Врем. зоны;
- Веер;
- Дуги;
- Расширения.
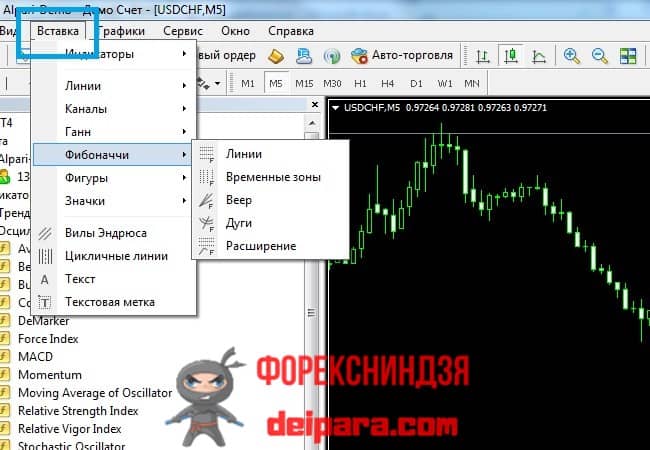
Рисунок 4. Нанести разметку на основе ряда Фибоначчи на график можно из меню «Вставка».Существуют и иные способы разметки графика на основе пропорций из чисел ряда Фибоначчи. Все они реализованы в виде индикаторов и требуют скачивания и установки в «Навигатор» терминала. После этого можно пользоваться такими более функциональными модернизированными алгоритмами (например, ICWR_a и QuickFib).
Квадраты и домино
Начнем с укладки квадратов и домино. Вообразим длинную горизонтальную рамку размерами 1 × 10. Мы хотим полностью заполнить ее квадратами 1 × 1 и костяшками домино 1 × 2, не оставив ни единой щели.
Для удобства обозначим число вариантов F10. Перебирать их все и потом пересчитывать — тяжелый труд, чреватый ошибками. Гораздо лучше упростить задачу. Не будем с места в карьер искать F10, начнем с F1. Это проще простого! Нам нужно заполнить рамку 1 × 1 квадратами 1 × 1 и костяшками домино 1 × 2. Домино не поместится, остается единственное решение: взять один квадрат. Другими словами, F1 = 1.
Теперь разберемся с F2. Размер рамки 1 × 2. Можно заполнить ее двумя квадратами или одной костяшкой домино. Таким образом, есть два варианта, и F2 = 2.
Дальше: сколькими способами можно заполнить рамку 1 × 3? Первый вариант: три квадрата. Два других варианта: одна костяшка домино (две не влезут) и квадрат слева или справа. Итак, F3 = 3. Еще один шаг: возьмем рамку 1 × 4. На рисунке показаны все варианты заполнения:
Мы нашли пять возможностей, но где гарантия, что мы ничего не упустили? Есть способ проверить себя. В левом конце рамки может быть или квадрат, или костяшка домино. В верхнем ряду на рисунке — варианты, когда слева квадрат, в нижнем ряду — когда слева домино.
Допустим, слева квадрат. Оставшуюся часть нужно заполнить квадратами и домино. Другими словами, нужно заполнить рамку 1 × 3. Это дает 3 варианта, так как F3 = 3. Если слева домино, размер оставшейся части 1 × 2, и заполнить ее можно двумя вариантами, так как F2 = 2.
Таким образом, у нас есть 3 + 2 = 5 вариантов, и мы удостоверились, что F4 = 5.
Теперь ваша очередь. Подумайте пару минут и найдите все варианты заполнения для рамки 1 × 5. Их немного. Решение — в конце главы. Можете отвлечься и подумать.
Вернемся к нашим квадратам. Хочется верить, что вы нашли 8 вариантов, так как есть 5 способов укладки, где слева квадрат, и еще 3 способа, где слева домино. Таким образом, F5 = 8.
Подытожим. Мы обозначили FN количество способов заполнения рамки 1 × n квадратами и костяшками домино. Нам необходимо найти F10. Вот что мы уже знаем:
Двигаемся дальше. Чему равно F6? Можно нарисовать все варианты, но это скучно. Лучше разобьем вопрос на две части. Сколькими способами можно заполнить рамку 1 × 6, если слева (a) квадрат и (b) костяшка домино? Хорошая новость: мы уже знаем ответ! В первом случае нам остается пять квадратов, а мы знаем, что F5 = 8. Во втором случае нужно заполнить четыре квадрата; нам известно, что F4 = 5. Таким образом, F5 + F4 = 13.
Чему равно F7? Исходя из тех же соображений, F7 =F6+F5=13+8=21. А как насчет F8? Очевидно, F8 = F7 + F6 = 21 + 13 = 34. И так далее. Мы обнаружили следующую взаимосвязь: Fn = Fn-1 + Fn-2.
Любопытные факты
Давайте ещё раз посмотрим на последовательность чисел Фибоначчи:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
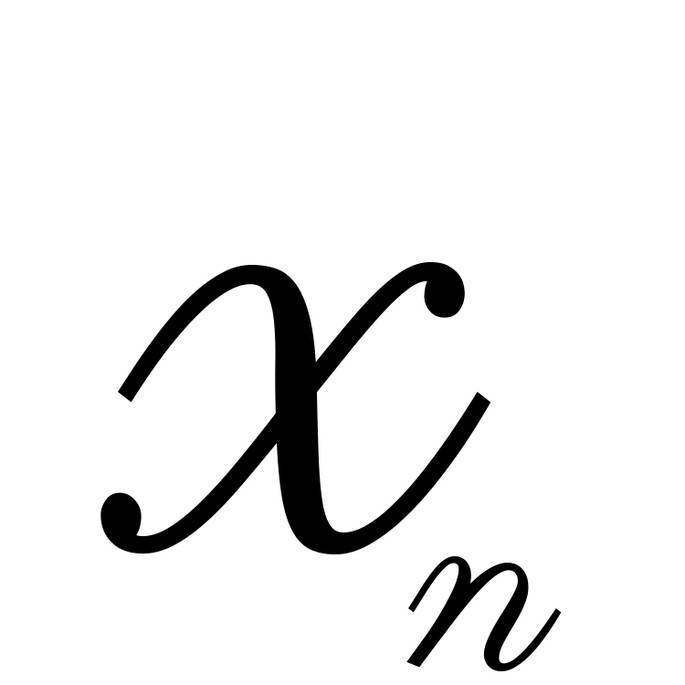 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 | 1597 |
Если внимательно посмотреть на цифры, можно рассмотреть удивительную закономерность:
- посмотрите на , а потом взгляните на последующие элементы: 6-ой, 9-ый, 12-ый… Каждый третий элемент делится на 2!
- посмотрите на , а потом взгляните на последующие элементы: 8-ой, 12-ый, 16-ый… Каждый четвёртый элемент делится на 3!
- посмотрите на , а потом взгляните на последующие элементы: 10-ый, 15-ый… Каждый пятый элемент делится на 5!
Первые 6 цифр Фибоначчи — 1/89
Если посчитать на калькуляторе 1 : 89 будет ответ 0,011235955… Заметили, что первые 6 цифр после запятой — ряд Фибоначчи?
День Фибоначчи 23/11
День Фибоначчи — 23 ноября (11/23; в американском формате дат месяц идёт первым, а день вторым), так как в нём присутствуют цифры “1, 1, 2, 3”, которые являются частью последовательности. 23 ноября можно всех поздравлять с Днём Фибоначчи!
Получение чисел Фибоначчи за время O(n)
Если n равно 1, то в качестве числа Фибоначчи будет напечатан только 0. Если n равно 2, то 0 и 1 будут напечатаны как числа Фибоначчи в указанном порядке. Если n равно 3, то 0, 1 и 1 будут напечатаны как числа Фибоначчи именно в таком порядке. Если n равно 4, то 0, 1, 1 и 2 будут напечатаны как числа Фибоначчи в указанном порядке. Если n равно 5, то 0, 1, 1, 2 и 3 будут напечатаны как числа Фибоначчи в указанном порядке. Если n равно 6, то 0, 1, 1, 2, 3 и 5 будут напечатаны как числа Фибоначчи именно в таком порядке — и так далее.
Функция Python для получения первых n чисел Фибоначчи:
Он начинается с создания массива из n элементов, инициализированных нулями. Этот массив будет содержать числа Фибоначчи. Первое число Фибоначчи, 0, уже есть. Второе число Фибоначчи, 1, присваивается следующим оператором (в функции). Затем идет цикл for, который начинается с индекса 2 и заканчивается непосредственно перед n. В нем есть утверждение:
Это добавляет два ближайших предыдущих числа.
Код для вызова функции и вывода первых двенадцати чисел Фибоначчи может быть таким:
N = 12 A = fibonacci(N) for i in range(N): print (A, end=’ ‘) print()
Результат:
Числа Фибоначчи
Одним из наиболее известных математических рекурсивных алгоритмов является последовательность Фибоначчи. Последовательность Фибоначчи можно увидеть даже в природе: ветвление деревьев, спираль раковин, плоды ананаса, разворачивающийся папоротник и т.д.
Спираль Фибоначчи выглядит следующим образом:
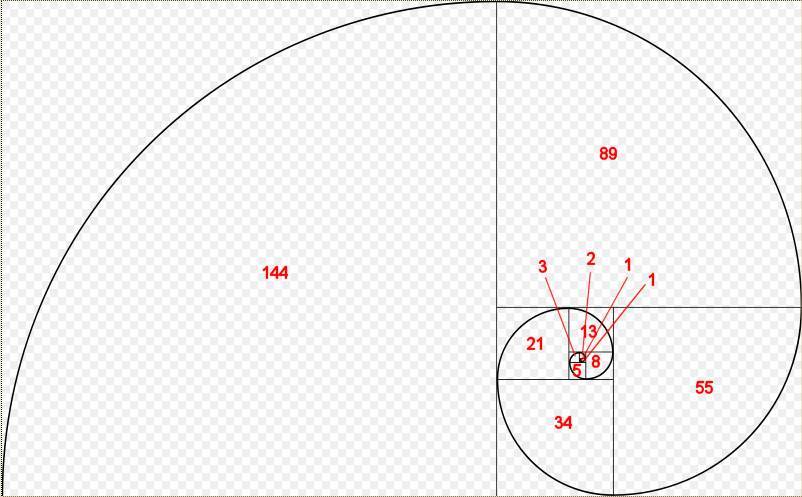
Каждое из чисел Фибоначчи — это длина горизонтальной стороны квадрата, в которой находится данное число. Математически числа Фибоначчи определяются следующим образом:
Следовательно, довольно просто написать рекурсивную функцию для вычисления n-го числа Фибоначчи:
1 | #include <iostream> intfibonacci(intnumber) if(number==) return// базовый случай (условие завершения) if(number==1) return1// базовый случай (условие завершения) returnfibonacci(number–1)+fibonacci(number–2) } // Выводим первые 13 чисел Фибоначчи intmain() for(intcount=count<13++count) std::cout<<fibonacci(count)<<” “ return } |
Результат выполнения программы выше:
Дуги
Из всех перечисленных инструментов, использующих в трейдинге уровни Фибоначчи, дуги имеют существенное отличие. При своем построении, они не только показывают места коррекции, но еще учитывают временной фактор. Это делает инструмент более универсальным.
Построение дуг не отличается от построения веера или сетки. Выглядят они как полукруг или эллипс (в случае соответствующей настройки). Зоны, образованные линиями, будут являться местами поиска коррекции.
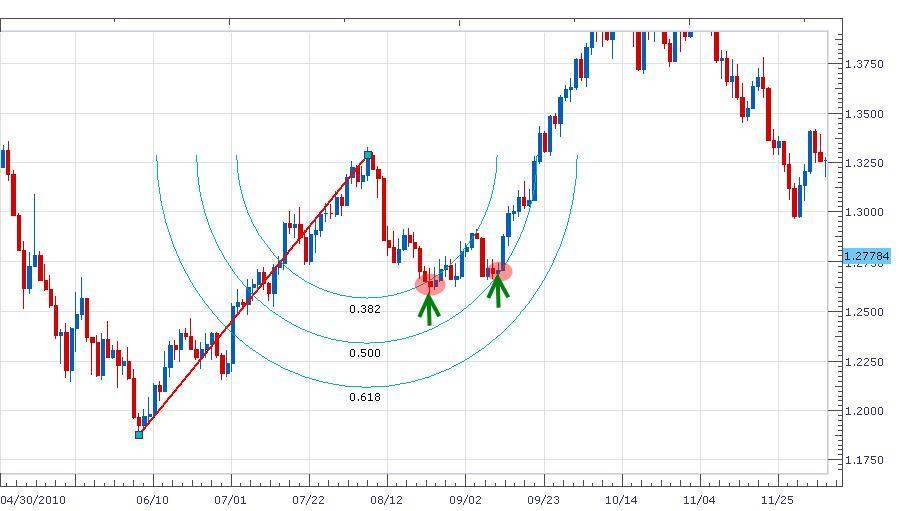
Нужно заметить, что хотя эллипс растянут по площади, он все же ограничен, в отличие от линий, построенных веером. Поэтому при выходе цены за пределы дуг, не нужно учитывать уровни, которые были построены. Скорее всего, за пределами эллипса возникнет зона флэта, или начала нового тренда.
Периодичность последовательности Фибоначчи по модулю
Рассмотрим последовательность Фибоначчи по некоторому модулю . Докажем, что она является периодичной, и причём период начинается с (т.е. предпериод содержит только ).
Докажем это от противного. Рассмотрим пар чисел Фибоначчи, взятых по модулю :
Поскольку по модулю может быть только различных пар, то среди этой последовательности найдётся как минимум две одинаковые пары. Это уже означает, что последовательность периодична.
Выберем теперь среди всех таких одинаковых пар две одинаковые пары с наименьшими номерами. Пусть это пары с некоторыми номерами и . Докажем, что . Действительно, в противном случае для них найдутся предыдущие пары и , которые, по свойству чисел Фибоначчи, также будут равны друг другу. Однако это противоречит тому, что мы выбрали совпадающие пары с наименьшими номерами, что и требовалось доказать.
Коэффициент чисел Леонардо Фибоначчи и % отношения уровня коррекции.
Как мы уже говорили, многие методы анализа биржи Форекс, основаны на последовательном ряде уровней Фибоначчи.
Так как из 3-х волн удлиняется как правило одна, две другие остаются одинаковыми по размеру и времени завершения.
В том случае, когда удлиняется волна 5, первая и третья, в большинстве случаев остаются практически одинаковыми.
Если растягивается третья, приближенно равными остаются первая и пятая.
Наименьшим показателем пика третьей волны должна быть точка. Ее числовые координаты вычисляют следующим образом:
- умножают размер (длину) первой волны, на число из ряда Фибоначчи — 1, 618,
- потом суммируют произведение этих чисел к показателю начала второй, (т. е. к значению, аналогичному наименьшей ее точке).
Верхний пик пятой, будет установлен порядком произведения размера первой на 3, 236 (т. е. это 2 * 1, 618). Выведенный результат, необходимо сложить со значением наивысшей точки или с основанием первой волны. В итоге, у нас получится минимальный или максимальный порядковый ориентир.
После того как, первая и третья волны будут равны, а пятая станет более длинной, тогда наш ориентир цены, можно рассчитать так:
Для начала, необходимо замерить дистанцию от наименьшей точки первой волны, до пика третьей, полученный результат надо умножить на — 1, 618.
Данное произведение, следует суммировать со значением наименьшей точки четвертой волны.
Во время коррекции тренда, если происходит стандартная зигзагообразная коррекции вида 5, 3, 5, как правило, волна С вырастает до уровня длины А.
Предполагаемый размер С, можно рассчитать, произведением числа 0, 618 и размера волны А, в последующем вычтя рассчитанное число из минимального значения А.
При горизонтальной коррекции вида 3, 3, 5, в то время когда В вырастает до уровня пика А, или возможно даже перекрывает его, С должна быть приблизительно равной такому значению — 1, 618 размера А. В соразмерном треугольнике каждая вновь идущая волна, относительно предшествующей, будет колебаться около этого значения — 0, 618.
ТОП БРОКЕРОВ ОПЦИОНОВ, ПРИЗНАННЫХ НЕЗАВИСИМЫМИ РЕЙТИНГАМИ
Выплаты автоматом. Без верификации! | обзор | отзывы | НАЧАТЬ С $10$
 Год основания 2012. Депозит с 300 рублей | обзор | отзывы | БОНУС 100% НА СЧЕТ
Год основания 2012. Депозит с 300 рублей | обзор | отзывы | БОНУС 100% НА СЧЕТ
Фиксированные опционы от ПАО Alpari | обзор | отзывы | ОПЦИОНЫ С 1 USD
ТОП ФОРЕКС БРОКЕРОВ РОССИЙСКОГО РЕЙТИНГА НА 2022 ГОД:
Что говорят трейдеры об АМаркетс? БОНУС 100% К СЧЕТУ | обзор/отзывы
Имею тут счет в 1050$. Платит с 1998 года! | 4 АКЦИИ И КОНКУРСА | обзор/отзывы
Взаимосвязь числового ряда Фибоначчи и теории Эллиота.
Полный цикл повышающего рыночного движения содержит восемь волн. Из которых пять — это рост, вслед за которыми идут три — спад.
Тренд на рынке условно можно разделить на пять волн, в течение предстоящей в иерархии, наиболее долго длящейся тенденции рынка.
Как правило, коррекция постоянно состоит из 3 скачков…
Обычная коррекция подразделяется на 2 вида:
- это зигзаг 5, 3, 5,
- а также плоская волна 3, 3, 5.
На четвертой, обычно формируются треугольники, которые постоянно предшествуют последней образовавшейся волне. Эта формация также может быть корректирующей волной В.
Всякая волна подразделяется на более маленькие и является составляющей более длинной.
Бывает так, что одна импульсная волна растягивается, а другие две как правило, должны быть одинаковыми по размеру и времени формирования.
Коэффициенты чисел Фибоначчи и отношения размеров коррекции, которые выведены с помощью этих чисел, применяются для нахождения ориентиров цены.
Взаимосвязь размера коррекции к предшествующему движению тренда, обычно равно: 62, 50, 38 процентам.
Метод чередования гласит: не следует дожидаться одного и того же проявления динамики цены 2 раза подряд.
Активный бычий рынок не может упасть ниже, чем начало предшествующей 4 волны.
Кроме того, 4 волна не должна пересекаться с первой.
Главными критериями теории Элиота выступают:
1) форма волны;
2) соотношение их длины;
3) период их развития.
Помимо этого, как мы уже упоминали, на последовательности выведенной Леонардо Фибоначчи, основывается еще много эффективных методов анализа на Форекс, которые обязательно будут затронуты в материалах этого сайта.
РЕКОМЕНДУЕМ ПОСМОТРЕТЬ:

Регистрация
основан в
2016
старт
от $10
ставка
$1
бонус
—
9,9
Обзор
Рекомендую попробовать ЭТУ АВТОРСКУЮ СТРАТЕГИЮ!!

Регистрация
основан в
2012
старт
300 ₽
ставка
60 ₽
бонус
30.000
9,6
Обзор
Стабильно платящий брокер опционов с 2012 года.

Регистрация
основан в
2007
старт
от $100
ставка
$1
бонус
15%
9,7
Обзор
Регистрация
основан в
1998
старт
$5
ставка
$1
бонус
% кешбэка
9,9
Обзор
100% бонус
основан в
2007
старт
$1
ставка
$1
бонус
100%
9,8
Обзор
| ТОРГОВЫЕ УСЛОВИЯ | СТРАТЕГИИ ДЛЯ INSTAFOREX |
Комбинаторное доказательство
А вот совершенно другое доказательство тождества F0 +F1 +F2 +…+Fn =Fn+2 –1.. Основной подход тут — воспользоваться тем фактом, что число Fn — это количество способов облицевать прямоугольник 1 × n квадратами и костяшками домино.
Напомню, что нам нужно доказать:
F0 + F1 + F2 +… + Fn = Fn+2- 1. (*)
Идея заключается в том, чтобы рассматривать обе части уравнения как решение задачи с облицовкой. Если мы докажем, что левая и правая часть — решение для одного и того же прямоугольника, они совпадут между собой. Эта техника носит название комбинаторного доказательстваСлово «комбинаторный» образовано от существительного «комбинаторика» — названия раздела математики, предметом которого является подсчет вариантов в задачах, схожих с облицовкой прямоугольника. Слово «комбинаторика», в свою очередь, образовано от слова «комбинации»..
На какой вопрос по комбинаторике уравнение F0 +F1 +F2 +…+Fn =Fn+2 –1. дает два верных ответа? Эта головоломка похожа на те, что встречаются в шоу Jeopardy! Популярная в США телевикторина. Аналоги Jeopardy! выходят в разных странах; в России это — «Своя игра». — Прим. ред., где участники должны формулировать вопрос, заранее зная правильный ответ.
Правая часть выглядит проще, поэтому начнем с нее. Ответ: Fn+2– 1. Каков вопрос? Если бы ответ был равен просто Fn+2, мы с легкостью сформулировали бы вопрос: сколькими способами можно облицевать прямоугольник 1 × (n + 2) с помощью квадратов и костяшек домино? Это почти то, что нужно, но ответ меньше на единицу. Попробуем мягко поменять вопрос и уменьшить ответ. Уберем один вариант облицовки и пересчитаем оставшиеся. Сложность состоит в том, чтобы найти один вариант, который кардинально отличается от остальных. Есть ли такой?
Каждый способ облицовки подразумевает использование квадратов или домино. Только квадраты задействованы в единственном варианте, в прочих есть хотя бы одна костяшка домино. Возьмем это за основу нового вопроса.
Вопрос: Сколько существует вариантов облицовки квадратами и костяшками домино прямоугольной рамки 1 × (n + 2), включающих по меньшей мере одну костяшку домино?
Сейчас мы найдем два ответа на этот вопрос. Так как оба будут верны, между числами мы сможем уверенно поставить знак равенства.
Один из ответов мы уже обсуждали. Есть Fn+2 вариантов укладки. Только один из них подразумевает использование исключительно квадратов, без домино. Таким образом, ответ № 1 на наш вопрос таков: Fn+2– 1.
Второй ответ должен быть — я надеюсь — левой частью уравнения F0 +F1 +F2 +…+Fn =Fn+2 –1.. Посмотрим, как это работает.
Нужно пересчитать варианты заполнения рамки, включающие хотя бы одну костяшку домино. Давайте подумаем, где будет расположена самая первая костяшка. Есть n + 2 позиций, и первая костяшка может располагаться в позициях от 1 до n + 1.
Рассмотрим случай n = 4. Мы ищем варианты заполнения рамки 1 × 6, задействующие хотя бы одну костяшку домино. Мы знаем ответ: F6 — 1 = 13 — 1 = 12, но нам необходимо получить его иным путем.
Первая костяшка домино может занимать следующие позиции:
Первая колонка демонстрирует случай, когда костяшка находится на первой позиции, вторая — когда костяшка на второй, и т. д.
Сколько вариантов в каждой колонке?
В первой колонке — пять вариантов. Если отбросить домино слева, мы получим ровно F4 = 5 вариантов для прямоугольника 1 × 4. Во второй колонке — три варианта. Отбросим домино и квадрат слева. Мы получим F3 = 3 варианта для прямоугольника 1 × 3. Аналогично для других колонок. Вот что мы обнаружили:
Таким образом, количество способов замостить квадратами и домино (хотя бы одной костяшкой) прямоугольную рамку 1 × 6 равно F4 + F3 + F2 + F1 + F0 = 12.
Вывод: F0+F1+F2+F3+F4=12=F6–1.
Рассмотрим общий случай. Нам дана рамка длиной n + 2. Сколько есть вариантов ее заполнения, при которых первая костяшка домино находится на некой позиции k? В этом случае первые k — 1 позиций заняты квадратами. Таким образом, в общей сложности занята k + 1 позиция Число k может принимать значения от 1 до n + 1, но не больше, потому что иначе последняя костяшка домино высунется за пределы рамки.. Оставшиеся (n + 2) — (k + 1) = n — k + 1 можно заполнить любыми способами. Это дает Fn-k+1 вариантов. Построим диаграмму:
Если k меняется от 1 до n + 1, величина n — k + 1 меняется от 0 до n. Таким образом, количество вариантов заполнения нашей рамки с использованием хотя бы одной костяшки домино равно Fn + Fn-1 +… + F1 + F0.
Если поставить слагаемые в обратном порядке, мы получим левую часть выражения (*). Таким образом, мы нашли второй ответ на поставленный вопрос: F0 +F1 +…+Fn.
Итак, у нас есть два ответа на вопрос. Величины, полученные с помощью двух выведенных нами формул, совпадают, и тождество F0 +F1 +F2 +…+Fn =Fn+2 –1. доказано.
Значение уровней в трейдинге
Уровни Фибоначчи применяются в нескольких инструментах, которые используют трейдеры в торговых стратегиях.
Первый важный уровень сетки Фибо – 0,318 – образуется, как число, поделенное на стоящее через одно в последовательности Фибоначчи.
Итак, принцип построения чисел золотого сечения понятен. Рассмотрим, что представляет собой сетка Фибоначчи.
- Уровни коррекции: 0.236, 0.382, 0.500, 0.618, 0.764.
- Уровни расширения: 0, 0.382, 0.618, 1.000, 1.382, 1.618
Многие трейдеры считают, что раз эти соотношения являются элементами всеобщей гармонии, так почему не использовать их для определения уровней коррекции Фибоначчи?
Во время поступательного движения цены, неизбежно возникают откаты. В этих местах цена делает передышку, после чего продолжается движение. От того, насколько глубоким был откат, можно определить величину последующего хода. Для этого и нужны уровни Фибоначчи, а также для того, чтобы точно установить величину коррекции и на соответствующем расширении, выставить take profit. Кроме того, их можно использовать для выставления стоп-приказа, ограничивающего убытки.
Итеративный метод
Вы можете увидеть, что применение рекурсивного решения проблемы в компьютерной науке часто рассматривается как халатность, а итеративные методы считаются намного лучше. Для генерации чисел Фибоначчи мы можем создать итеративное решение:
Мы можем воспользоваться им, чтобы вычислить любое число Фибоначчи (я не тестировал подход с особенно большими числами), и часто этот подход работает также очень быстро, 1000-е число вычислилось всего за 0,0028195 секунды.
Вы можете задаться вопросом, почему нельзя воспользоваться этим подходом для вычисления 1000000-го числа, и да, это возможно, но займёт немного времени. Продолжайте читать, и я расскажу, почему.
Как появились числа и их производные
Решая прикладную задачу, Леонардо наткнулся на любопытный ряд чисел Фибоначчи, вначале которого находятся две единицы.
Каждый последующий член – это сумма двух предыдущих. Самое любопытное, что числовой ряд Фибоначчи – примечательная последовательность тем, что если любой член поделить на предыдущий, то получится число, которое близко к 0,618. Этому числу дали имя «Золотое сечение».
Оказалось, что это число было известно человечеству очень давно. Например, в древнем Египте строили пирамиды с его использованием, а древние греки возводили по нему свои храмы. Леонардо да Винчи показал, как строение тела человека подчиняется этом числу.
Природа применяет числа из ряда Фибоначчи в своих наиболее сокровенных и продвинутых областях. От атомных структур и других мелких форм, как молекулы ДНК и микрокапилляры мозга до огромных, как планетарные орбиты и структуры галактик. Ряд примеров настолько велик, что следует утверждать, что в природе действительно присутствует некий основной закон пропорций.
Поэтому не удивительно, что ряд Фибоначчи и золотое сечение пробралось и на биржевые графики. И не одно число 0,618, но и его производные.
Если число золотого сечения возвести в первую, вторую, третью и четвертую степень и вычесть результат из единицы, то получиться новый ряд, который носит название «коэффициенты коррекции Фибоначчи». Осталось только добавить отметку пять десятых – это пятидесятипроцентная коррекция Чарльза Доу.
Однако, это не все, что можно сделать с золотым сечением. Если единицу разделить на 0,618 то получается 1,618, если возведем в квадрат, то у нас получится 2,618, если возведем в куб, то получим число 4,236. Это коэффициенты расширения Фибоначчи. Тут не хватает только числа 3,236, которое было предложено Джоном Мёрфи.
Стратегия с использованием Фибо
Торговых стратегий на уровнях Фибоначчи великое множество. Рассмотрим вариант под названием Magic Grid. Это простая консервативная стратегия, которая показывает соотношение прибыли к убыткам 56%. Действия трейдера сводятся к тому, чтобы правильно настроить индикаторы и выставить стоп-приказы, ограничивающие убытки и фиксирующие прибыль.
Для работы используются два индикатора Moving average и сетка Фибоначчи. Метод построения скользящих средних простой (simple), и обе применяются к закрытию свечи (close). У одной будет период 100, у другой – 200. Пересечение этих скользящих скажут о сформировавшемся тренде. Стратегия используется на часовом и 4-часовом таймфрейме.
В терминале Metatrader инструмент сетка называется Линии Фибоначчи. Его нужно будет подкорректировать, добавив уровень 76,4. Делается это следующим способом. Кликнуть 2 раза по сетке, после этого она перейдет в активное состояние. Затем правой кнопкой мыши вызвать меню инструмента. Нужно выбрать “Уровни”. На этой вкладке следует добавить новый уровень – 0,764. В графе “Описание” записать 76,4. Затем нужно сохранить изменения.
В стратегии используются 2 сетки. Поэтому лучше каждую из них помечать своим цветом, чтобы не перепутать уровни. Сделать это можно там же в свойствах инструмента.
Рассмотрим, как торговать по уровням Фибоначчи на примере восходящего тренда.
При пересечении быстрой скользящей с периодом 100 медленную скользящую, устанавливаем наличие бычьего тренда.
Следующим этапом нужно дождаться начала коррекции. Это можно определить по нескольким факторам:
- Тренд выходит из своего коридора.
- Верхушки свечей (high) перестают обновляться.
- Нижние тени свечей стремятся обновить предыдущие тени.
- Индикаторы RSI, Stochastic могут показывать зону перекупленности.
Нужно построить уровни Фибоначчи, как только началась коррекция тренда. Для этого натягивается сетка № 1 от минимального значения тренда до максимального. Минимум будет точкой “A”, а максимум – точкой “B”.
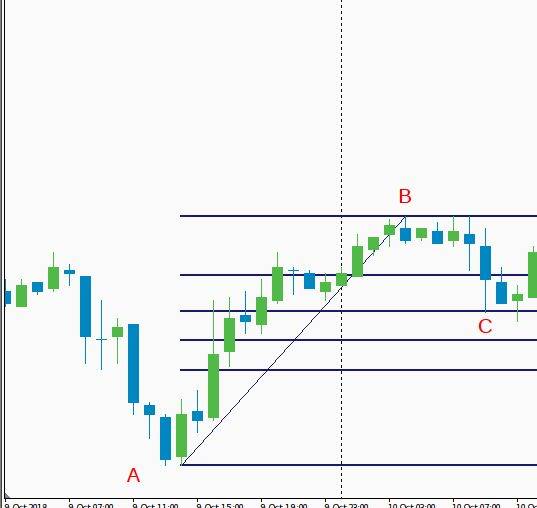
Как только откат достигнет уровня 38,2 и выше, из точки “B” тянется сетка № 2 в противоположном направлении, то есть в сторону коррекции до ее окончания. Это будет точкой “C”.
Вход в сделку по направлению тренда осуществляется на уровне 76,4 сетки № 2. Первая цель фиксации прибыли устанавливается также по второй сетке на уровне 161,8. Stop loss выставляется ниже точки “C” на несколько пунктов.
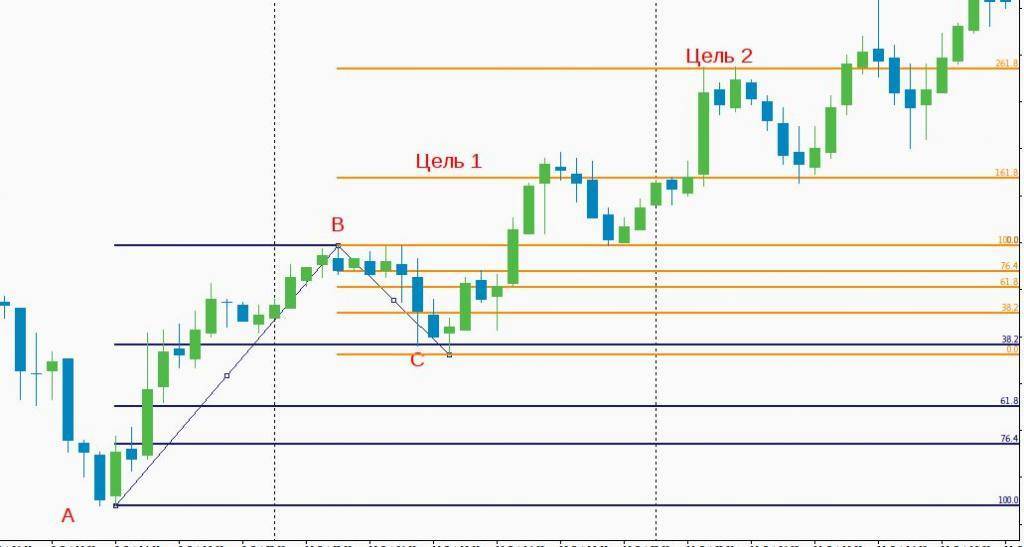
В дополнение к этой стратегии можно сказать, что если коррекция не дошла до уровня 38,2, то откат не торгуется. Если цена пробила уровень 76,4, то данная коррекция рассматривается, как медвежий тренд. Точка “В” становится точкой “А”, точка “C” будет точкой”B”. При пробое уровня 76,4, рассматриваются сделки на продажу.
Простая рекурсия
Это очень простой способ получить N-ное число Фибоначчи на Python:
В коде используется рекурсия, он вызывает сам себя несколько раз, вычисляя предыдущее число и используя это число для вычисления следующего. Но это также недостаток, поскольку функция чрезвычайно неэффективна и ресурсоёмка: на каждом этапе она вычисляет предыдущие 2 числа, а также предыдущие 2 числа этих чисел и т. д.
Вскоре вы достигаете точки, когда вычисление следующего числа занимает слишком много времени, например, на моём компьютере мне потребовалось 1,43 секунды, чтобы вычислить 35-е число. Очевидно, что вычисление более высоких значений будет чрезвычайно медленным и практически невозможным.
Числа Фибоначчи в визуальном искусстве и дизайне
Золотая спираль, основанная на последовательности чисел Фибоначчи, является одним из универсальных принципов построения пропорций. Лежащее в ее основе золотое сечение было известно еще в государствах Древнего Востока, но особую популярность оно приобрело в эпоху Возрождения. Великие скульпторы и живописцы того времени начали применять золотую спираль для построения художественной композиции, пропорций различных объектов, в том числе человеческого тела. Золотое сечение сегодня используется как одна из моделей для гармоничного распределения объектов в кадре (в фото- и киноискусстве), элементов плакатов и т.д.
В компьютерную эру золотое сечение (золотая спираль) и числа Фибоначчи также нашли свое применение в визуальном искусстве, в частности, 2D/3D-моделировании и веб-дизайне:
Решетка Фибоначчи применяется для эффективного наложения точек на двухмерные и трехмерные объекты, например сферу или многогранники. Таким способом можно выполнить высокоточную огранку ювелирных камней или построить визуальную модель молекулярных решеток некоторых веществ.

Решетка Фибоначчи на трехмерной фигуре (сфере)
- На основе числовой последовательности Фибоначчи строится один из вариантов фракталов — самоподобных фигур. Эту математическую модель можно использовать в компьютерной графике для построения ветвящихся объектов (ветвей, корней деревьев, русел рек, кристаллов и т. д.).
- Золотое сечение применяется в веб-дизайне для разметки страниц некоторых сайтов или веб-приложений. Элементы интерфейса, организованные таким способом, образуют визуально привлекательную и удобную рабочую область.
- Фрактальная геометрия, основанная в том числе на закономерности Фибоначчи, является самостоятельным направлением визуального искусства. Она применяется в аудиовизуальных инсталляциях, мэппингах и т.д.