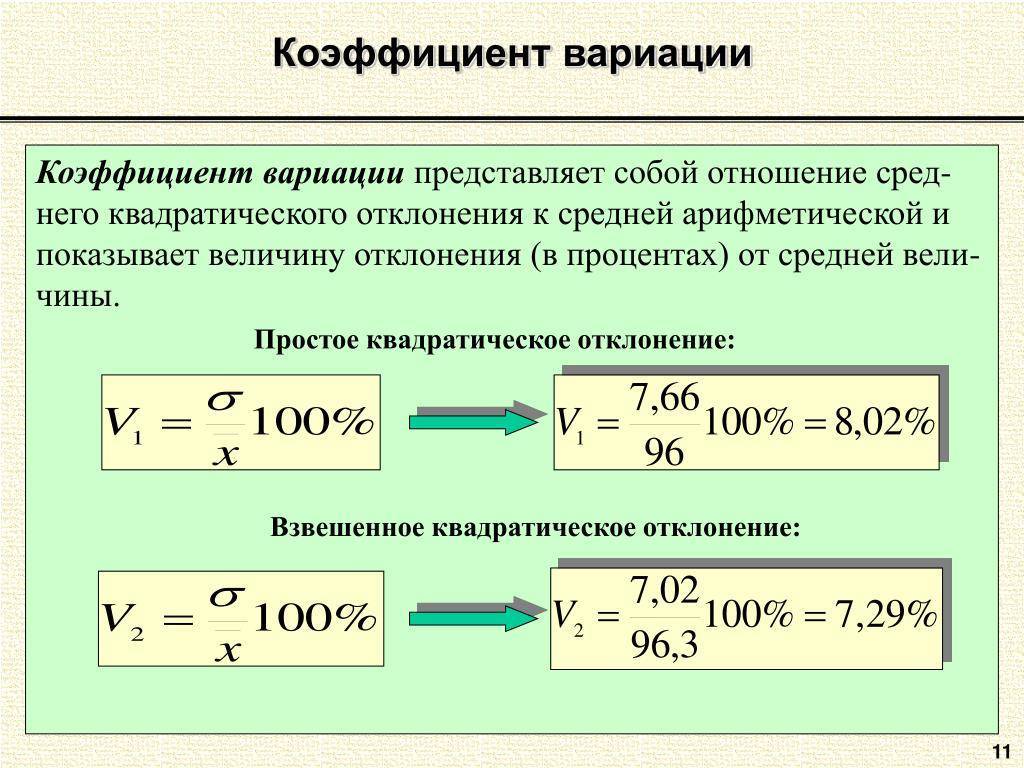
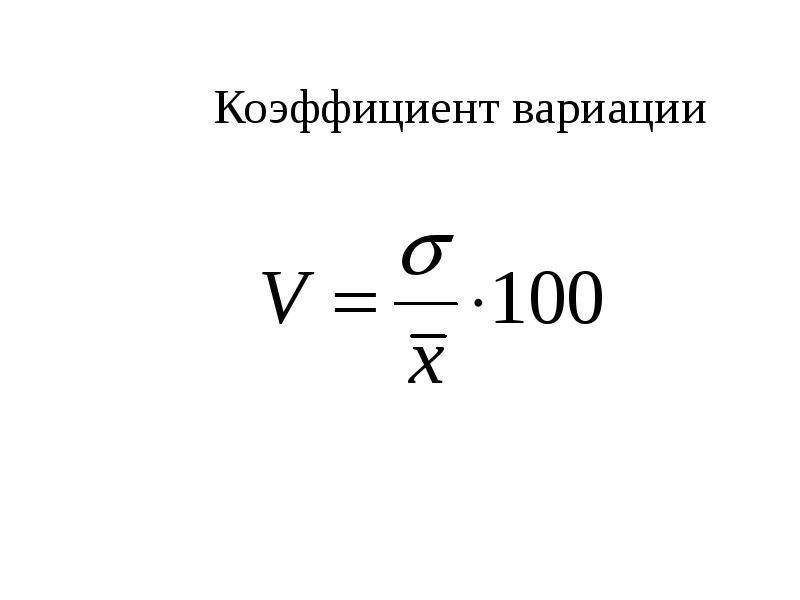Коэффициент вариации в статистике: примеры расчета
Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.
- Показатели описательной статистики
- Среднее арифметическое
- Стандартное отклонение
- Коэффициент вариации
- Расчёты в Microsoft Ecxel 2016
Среднее арифметическое
Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):
168, 171, 175, 177, 179, 187, 174, 176, 179, 169.
Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:
- Ширина интервала, куда попадает рост всех студентов, – 18 см.
- В распределении рост наиболее близок к середине этого интервала.
- Встречаются и исключения, которые наиболее близко расположены к верхней или нижней границе интервала.
Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться.
Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического.
Если обратиться к росту студентов, то формула будет выглядеть следующим образом:
Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)
Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).
Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.
Стандартное отклонение
Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.
На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:
Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:
Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:
Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.
Расчёты в Microsoft Ecxel 2016
Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:
| Наименование показателя | Расчёт в Excel 2016* |
| Среднее арифметическое | =СРГАРМ(A1:A10) |
| Дисперсия | =ДИСП.В(A1:A10) |
| Среднеквадратический показатель | =СТАНДОТКЛОН.В(A1:A10) |
| Коэффициент вариации | =СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10) |
| Коэффициент осцилляции | =(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10) |
* — в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.
Итак, обобщим информацию:
- Среднее арифметическое – это значение, позволяющее найти среднее значение показателя в ряду данных.
- Дисперсия – это среднее значение отклонений возведенное в квадрат.
- Стандартное отклонение (среднеквадратичное отклонение) – это корень квадратный из дисперсии, для приведения единиц измерения к одинаковым со среднеарифметическим.
- Коэффициент вариации – значение отклонений от среднего, выраженное в относительных величинах (%).
Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила — коэффициент вариации, который является мерой однородности данных.
Упражнение 3.
Смотритель парка подозревает, что популяции черных и белых кроликов в его парке не имеют одинаковой изменчивости в размерах. Чтобы продемонстрировать это, он взял образцы по 25 кроликов из каждой популяции и получил следующие результаты:
– Белые кролики: средний вес 7,65 кг и стандартное отклонение 2,55 кг. -Черные кролики: средний вес 6,00 кг и стандартное отклонение 2,43 кг.
Смотритель парка прав? Ответ на гипотезу смотрителя парка можно получить с помощью коэффициента вариации: Ответ: коэффициент вариации веса черных кроликов почти на 7% больше, чем у белых кроликов, поэтому можно сказать, что смотритель парка прав в своем подозрении, что вариабельность веса двух популяций кроликов не равны.
Расчет показателей вариации в Excel
Оригинал http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel
Добрый день, уважаемые любители статистического анализа данных, а сегодня еще и программы Excel.
Проведение любого статанализа немыслимо без расчетов. И сегодня в рамках рубрики «Работаем в Excel» мы научимся рассчитывать показатели вариации. Теоретическая основа была рассмотрена ранее в ряде статей о вариации данных.
Кстати, на этом указанная тема не закончилась, к выпуску планируются новые статьи – следите за рекламой! Однако сухая теория без инструментов реализации – вещь не сильно полезная.
Поэтому по мере появления теоретических выкладок, я стараюсь не отставать с заметками о соответствующих расчетах в программе Excel.
Сегодняшняя публикация будет посвящена расчету в Excel следующих показателей вариации:
— максимальное и минимальное значение
— среднее линейное отклонение
— дисперсия (по генеральной совокупности и по выборке)
— среднее квадратическое отклонение (по генеральной совокупности и по выборке)
— коэффициент вариации
Факт возможности расчета упомянутых показателей в Excel свидетельствует о практическом их использовании. И, несмотря на очевидность некоторых моментов, я постараюсь расписать все подробно.
Максимальное и минимальное значение
Начнем с формул максимума и минимума. Что такое максимальное и минимальное значение, уверен, знают почти все. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое (может быть и отрицательным числом).
Это крайние значения в совокупности данных, обозначающие границы их вариации. Примеры реального использования каждый может придумать сам – их полно. Это и минимальные/максимальные цены на что-нибудь, и выбор наилучшего или наихудшего решения задачи, и всего, чего угодно.
Минимум и максимум – весьма информативные показатели. Давайте теперь их рассчитаем в Excel.
Выбираем нужную формулу, в следующем окошке указываем диапазон данных (в котором ищется максимальное или минимальное значение) и жмем «ОК».
Функции МАКС и МИН достаточно часто используются, поэтому разработчики Экселя предусмотрительно добавили соответствующие кнопки в ленту. Они находятся там же, где суммаи среднее значение – в разворачивающемся списке.
В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической. Все архипросто.
Среднее линейное отклонение
Среднее линейное отклонение, напоминаю, представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:
где
a – среднее линейное отклонение,
x – анализируемый показатель, с черточкой сверху – среднее значение показателя,
n – количество значений в анализируемой совокупности данных.
В Excel эта функция называется СРОТКЛ.
После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК». Наслаждаемся результатом.
Среднее квадратическое отклонение
Среднеквадратическое отклонение по генеральной совокупности – это корень из генеральной дисперсии.
Выборочное среднеквадратическое отклонение – это корень из выборочной дисперсии.
Для расчета можно извлечь корень из формул дисперсии, указанных чуть выше, но в Excel есть и готовые функции:
— Среднеквадратическое отклонение по генеральной совокупности СТАНДОТКЛОН.Г
— Среднеквадратическое отклонение по выборке СТАНДОТКЛОН.В.
Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднее квадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.
Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
- одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
- двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
- трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Оценка
Когда только образец данных из доступна генеральная совокупность, CV генеральной совокупности можно оценить с помощью отношения s {\ displaystyle s \,}к выборочному среднему x ¯ {\ displaystyle {\ bar {x}}}:
- cv ^ = sx ¯ {\ displaystyle {\ widehat {c _ {\ rm {v}}}} = {\ frac {s} {\ bar {x}} }}
Но эта оценка, применяемая к выборке небольшого или среднего размера, имеет тенденцию быть слишком низкой: это смещенная оценка. Для нормально распределенных данных несмещенная оценка для выборки размера n:
- cv ^ ∗ = (1 + 1 4 n) cv ^ {\ displaystyle {\ widehat {c _ {\ rm { v}}}} ^ {*} = {\ bigg (} 1 + {\ frac {1} {4n}} {\ bigg)} {\ widehat {c _ {\ rm {v}}}}}
Логарифмически нормальные данные
Во многих приложениях можно предположить, что данные распределены логарифмически нормально (о чем свидетельствует наличие асимметрии в выборочных данных). В таких случаях более точная оценка, полученная на основе свойств логнормального распределения, определяется как:
- cv ^ raw = esln 2-1 {\ displaystyle {\ widehat {cv} } _ {\ rm {raw}} = {\ sqrt {\ mathrm {e} ^ {s _ {\ rm {ln}} ^ {2}} – 1}}}
где sln {\ displaystyle {s _ {\ rm {ln}}} \,}- стандартное отклонение выборки данных после преобразования натуральный логарифм. (В случае, если измерения записываются с использованием любой другой логарифмической основы, b, их стандартное отклонение sb {\ displaystyle s_ {b} \,}преобразуется в базу e с использованием sln = sb ln (b) {\ displaystyle s _ {\ rm {ln}} = s_ {b} \ ln (b) \,}и формула для cv ^ raw {\ displaystyle {\ widehat {cv}} _ {\ rm {raw}} \,}остается прежним.) Эту оценку иногда называют “геометрической CV” (GCV), чтобы отличить ее от простая оценка выше. Однако Кирквуд также определил «геометрический коэффициент вариации» как:
- GCVK = esln – 1 {\ displaystyle \ mathrm {GCV_ {K}} = {\ mathrm {e} ^ {s _ {\ rm {ln }}} \! \! – 1}}
Этот термин был задуман как аналог коэффициента вариации для описания мультипликативной вариации логнормальных данных, но это определение GCV не имеет теоретической основы для оценки cv {\ displaystyle c _ {\ rm {v}} \,}сам.
Для многих практических целей (таких как определение размера выборки и вычисление доверительных интервалов ) это sln {\ displaystyle s_ {ln} \,}, который наиболее часто используется в контексте нормально распределенных данных. При необходимости это можно получить из оценки c v {\ displaystyle c _ {\ rm {v}} \,}или GCV путем инвертирования соответствующей формулы.
Прогнозируем с Excel: как посчитать коэффициент вариации
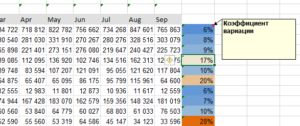
Каждый раз, выполняя в Excel статистический анализ, нам приходится сталкиваться с расчётом таких значений, как дисперсия, среднеквадратичное отклонение и, разумеется, коэффициент вариации.
Именно расчёту последнего стоит уделить особое внимание
Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений
Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений. В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных. В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных
В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных
Что такое коэффициент вариации и для чего он нужен?
Итак, как мне кажется, нелишним будет провести небольшой теоретический экскурс и разобраться в природе коэффициента вариации.
Этот показатель необходим для отражения диапазона данных относительно среднего значения. Иными словами, он показывает отношение стандартного отклонения к среднему значению.
Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.
Так, если вы видите, что значение коэффициента равно 0%, то с уверенностью заявляйте о том, что ряд является однородным, а значит, все значения в нём равны один с другим.
В случае, если коэффициент вариации принимает значение, превышающее отметку в 33%, то это говорит о том, что вы имеете дело с неоднородным рядом, в котором отдельные значения существенно отличаются от среднего показателя выборки.
Как найти среднее квадратичное отклонение?
Поскольку для расчёта показателя вариации в Excel нам необходимо использовать среднее квадратичное отклонение, то вполне уместно будет выяснить, как нам посчитать этот параметр.
Из школьного курса алгебры мы знаем, что среднее квадратичное отклонение — это извлечённый из дисперсии квадратный корень, то есть этот показатель определяет степень отклонения конкретного показателя общей выборки от её среднего значения. С его помощью мы можем измерить абсолютную меру колебания изучаемого признака и чётко её интерпретировать.
Рассчитываем коэффициент в Экселе
К сожалению, в Excel не заложена стандартная формула, которая бы позволила рассчитать показатель вариации автоматически. Но это не значит, что вам придётся производить расчёты в уме. Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.
Вставьте формулу и укажите диапазон данных
Для того чтобы рассчитать показатель вариации в Excel, необходимо вспомнить школьный курс математики и разделить стандартное отклонение на среднее значение выборки. То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.
Не забывайте и о том, что поскольку коэффициент выражается в процентах, то ячейке с формулой нужно будет задать соответствующий формат. Сделать это можно следующим образом:
- Откройте вкладку «».
- Найдите в ней категорию «Формат ячеек» и выберите необходимый параметр.
Как вариант, можно задать процентный формат ячейке при помощи клика по правой кнопке мыши на активированной клеточке таблицы. В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.
Выберите «Процентный», а при необходимости укажите число десятичных знаков
Возможно, кому-то вышеописанный алгоритм покажется сложным. На самом же деле расчёт коэффициента так же прост, как сложение двух натуральных чисел. Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.
Всё ещё не можете сделать качественное сравнение степени разброса данных? Теряетесь в масштабах выборки? Тогда прямо сейчас принимайтесь за дело и осваивайте на практике весь теоретический материал, который был изложен выше! Пусть статистический анализ и разработка прогноза больше не вызывают у вас страха и негатива. Экономьте свои силы и время вместе с табличным редактором Excel.
Аналогичные отношения
Стандартизованные моменты – аналогичные отношения, μ k / σ k {\ displaystyle {\ mu _ {k}} / {\ sigma ^ {k}}}где μ k {\ displaystyle \ mu _ {k}}- момент k относительно среднего, которые также безразмерны и масштабный инвариант. Отношение дисперсии к среднему, σ 2 / μ {\ displaystyle \ sigma ^ {2} / \ mu}- еще одно аналогичное соотношение, но не безразмерное. и, следовательно, не масштабно инвариантны. См. Нормализация (статистика) для дальнейших соотношений.
В обработке сигналов, в частности обработке изображений, обратное отношение μ / σ {\ displaystyle \ mu / \ sigma}(или его квадрат) упоминается как отношение сигнал / шум в целом и отношение сигнал / шум (отображение) в частности.
Другие связанные коэффициенты включают:
- , σ 2 / μ 2 {\ displaystyle \ sigma ^ {2} / \ mu ^ {2}}
- стандартизованный момент, μ k / σ k {\ displaystyle \ mu _ {k} / \ sigma ^ {k}}
- Отношение дисперсии к среднему (или относительная дисперсия), σ 2 / μ {\ displaystyle \ sigma ^ {2} / \ mu}
- фактор Фано, σ W 2 / μ W {\ displaystyle \ sigma _ {W} ^ {2} / \ mu _ {W}}(оконный VMR)
Интерпретация результатов
Прежде чем включить в инвестиционный портфель дополнительный актив, финансовый аналитик должен обосновать свое решение. Один из способов – расчет коэффициента вариации.
Ожидаемая доходность ценных бумаг составит:
Среднеквадратическое отклонение доходности для активов компании А и В составляет:
Ценные бумаги компании В имеют более высокую ожидаемую доходность. Они превышают ожидаемую доходность компании А в 1,14 раза. Но и инвестировать в активы предприятия В рискованнее. Риск выше в 1,7 раза. Как сопоставить акции с разной ожидаемой доходностью и различным уровнем риска?
Для сопоставления активов двух компаний рассчитан коэффициент вариации доходности. Показатель для предприятия В – 50%, для предприятия А – 33%. Риск инвестирования в ценные бумаги фирмы В выше в 1,54 раза (50% / 33%). Это означает, что акции компании А имеют лучшее соотношение риск / доходность. Следовательно, предпочтительнее вложить средства именно в них.
Таким образом, коэффициент вариации показывает уровень риска, что может оказаться полезным при включении нового актива в портфель. Показатель позволяет сопоставить ожидаемую доходность и риск. То есть величины с разными единицами измерения.
Вариация
– это несовпадение значений одной и той же статистической величины у разных объектов в силу особенностей их собственного развития, а также различия условий, в которых они находятся. Вариация имеет объективный характер и помогает познать сущность изучаемого явления. Если средняя величина сглаживает индивидуальные различия, то вариация, наоборот, их подчеркивает, устанавливая типичность или не типичность найденной средней величины для конкретной статистической совокупности. Тем самым можно делать вывод о качественности подобранных статистических данных.
Вариация измеряется с помощью относительных величин, называемых коэффициентами вариации
и определяемых в виде отношения среднего отклонения к средней величине.
Поскольку среднее отклонение может определяться линейным и квадратическим способами, то соответствующими могут быть и коэффициенты вариации. Следовательно, коэффициенты вариации надо определять по формулам
–линейный;(1.28)
–
квадратический.(1.29)
Значения коэффициента вариации изменяются от 0 до 1 и чем ближе он к нулю, тем типичнее найденная средняя величина для изучаемой статистической совокупности, а значит и качественнее подобраны статистические данные. При этом критериальным значением коэффициента вариации служит 1/3.
То есть средняя величина считается типичной для данной совокупности при λ
0,333 или при ν
0,333. В ином случае средняя величина не типична и требуется пересмотреть статистическую совокупность с целью включения в нее более объективных статистических величин.
Обычно квадратический коэффициент вариации несколько (примерно на 25%) больше линейного, рассчитанные по одним и тем же данным. А значит возможен случай, когда λ
0,333 и ν
0,333, тогда необходимо взять среднюю из этих коэффициентов и по ее значению сделать окончательный вывод о не/типичности найденной средней величины.
С помощью линейного коэффициента вариации принципиальный вывод о типичности или не типичности средней величины можно получить проще и быстрее, чем с помощью квадратического. Однако квадратический коэффициент применяется чаще, так как существует несколько способов для вычисления дисперсии.
У такого способа оценки вариации есть и существенный недостаток. Действительно, пусть, например, исходная совокупность рабочих, имеющих средний стаж 15 лет, со стандартным отклонением σ
= 10 лет, «состарилась» еще на 15 лет. Теперь= 30 лет, а стандартное отклонение по-прежнему равно 10. Совокупность, ранее бывшая неоднородной (10/15*100 = 66,7%), со временем оказывается, таким образом, вполне однородной (10/30*100 = 33,3 %).
Поэтому возможен дополнительный анализ статистической совокупности с помощью коэффициента осцилляции
, определяемого по формуле
где R
– размах вариации в виде разности наибольшего и наименьшего значений в совокупности статистических величин. То есть
R = Хмах –Хmin,
(1.31)
где Xмax и Xmin – максимальное и минимальное значения в совокупности.
При упорядочении статистических величин в совокупности образуются группировочные интервалы. Тогда под обозначением ∆Х
понимается размах интервала, а среднее интервальное значение обозначается ХИ
.
В случае ориентировки только на квадратический коэффициент вариации могут применяться разные методы определения дисперсии.
Формула коэффициента вариации
Ниже приведена формула расчета коэффициента вариации:
CVзнак равноσμжчере:σзнак равностпдр парddévяTяоп μзнак равномеан\ begin {align} & \ text {CV} = \ frac {\ sigma} {\ mu} \\ & \ textbf {где:} \\ & \ sigma = \ text {стандартное отклонение} \\ & \ mu = \ текст {среднее} \\ \ конец {выровненный}Взаимодействие с другими людьмирезюмезнак равноμ
Обратите внимание, что если ожидаемая доходность в знаменателе формулы коэффициента вариации отрицательна или равна нулю, результат может ввести в заблуждение
Коэффициент вариации в Excel
Формулу коэффициента вариации можно выполнить в Excel, сначала используя функцию стандартного отклонения для набора данных. Затем вычислите среднее значение, используя предоставленную функцию Excel. Поскольку коэффициент вариации – это стандартное отклонение, деленное на среднее значение, разделите ячейку, содержащую стандартное отклонение, на ячейку, содержащую среднее значение.
Пример коэффициента вариации для выбора инвестиций
Например, рассмотрим не склонного к риску инвестора, который желает инвестировать в торгуемый на бирже фонд (ETF) , который представляет собой корзину ценных бумаг, отслеживающую индекс широкого рынка. Инвестор выбирает SPDR S&P 500 ETF, Invesco QQQ ETF и iShares Russell 2000 ETF. Затем он анализирует доходность и волатильность ETF за последние 15 лет и предполагает, что ETFs могут иметь доходность, аналогичную их долгосрочным средним показателям.
В иллюстративных целях для принятия решения инвестором используется следующая историческая информация за 15 лет:
- Если SPDR S&P 500 ETF имеет среднегодовую доходность 5,47% и стандартное отклонение 14,68%, коэффициент вариации SPDR S&P 500 ETF составляет 2,68.
- Если Invesco QQQ ETF имеет среднегодовую доходность 6,88% и стандартное отклонение 21,31%, коэффициент вариации QQQ равен 3,10.
- Если iShares Russell 2000 ETF имеет среднегодовую доходность 7,16% и стандартное отклонение 19,46%, коэффициент вариации IWM составляет 2,72.
Основываясь на приблизительных цифрах, инвестор может инвестировать либо в SPDR S&P 500 ETF, либо в ETF iShares Russell 2000, поскольку соотношение риска и прибыли примерно одинаково и указывает на лучшее соотношение риска и доходности, чем в Invesco QQQ ETF.
Характеристики формы распределения
Для получения представления о форме распределения используются показатели среднего уровня (средняя арифметическая, мода, медиана), показатели вариации, ассиметрии и эксцесса.
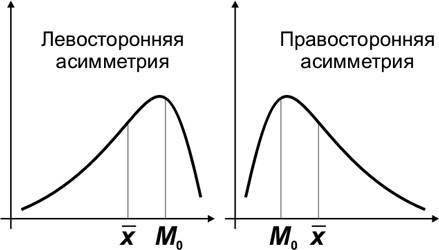
В симметричных распределениях средняя арифметическая, мода и медиана совпадают (. Если это равенство нарушается — распределение ассиметрично.
Простейшим показателем ассиметрии является разность , которая в случае правосторонней ассиметрии положительна, а при левосторонней — отрицательна.
Ассиметричное распределение
Для сравнения ассиметрии нескольких рядов вычисляется относительный показатель
В качестве обобщающих характеристик вариации используются центральные моменты распределения -го порядка , соответствующие степени, в которую возводятся отклонения отдельных значений признака от средней арифметической:
Для несгруппированных данных:
Для сгруппированных данных:
Момент первого порядка согласно свойству средней арифметической равен нулю .
Момент второго порядка является дисперсией .
Моменты третьего и четвертого порядков используются для построения показателей, оценивающих особенности формы эмпирических распределений.
С помощью момента третьего порядка измеряют степень скошенности или ассиметричности распределения.
— коэффициент ассиметрии
В симметричных распределениях , как все центральные моменты нечетного порядка.Неравенство нулю центрального момента третьего порядка указывает на асимметричность распределения. При этом, если , то асимметрия правосторонняя и относительно максимальной ординаты вытянута правая ветвь; если , то асимметрия левосторонняя (на графике это соответствует вытянутости левой ветви).
Для характеристики островершинности или плосковершинности распределения вычисляют отношение момента четвертого порядка () к среднеквадратическому отклонению в четвертой степени (). Для нормального распределения , поэтому эксцесс находят по формуле:
Для нормального распределения обращается в нуль. Для островершинных распределений , для плосковершинных .
Эксцесс распределения
Кроме показателей, рассмотренных выше, обобщающей характеристикой вариации в однородной совокупности служит определенный порядок в изменении частот распределения в соответствии с изменениями величины изучаемого признака, называемый закономерностью распределения.
Характер (тип) закономерности распределения может быть выявлен путем построения вариационного ряда на основании большого объема наблюдений, а также такого выбора числа групп и величины интегралов, при котором наиболее отчетливо могла бы проявиться закономерность.
Анализ вариационных рядов предполагает выявление характера распределения (как результата действия механизма вариации), установление функции распределения, проверку соответствия эмпирического распределения теоретическому.
Эмпирическое распределение, полученное на основе данных наблюдения, графически изображается эмпирической кривой распределения с помощью полигона.
На практике встречаются различные типы распределений, среди которых можно выделить симметричные и асимметричные, одновершинные и многовершинные.
Установить тип распределения, означает выразить механизм формирования закономерности в аналитической форме. Многим явлениям и их признакам свойственны характерные формы распределения, которые аппроксимируются соответствующими кривыми. При всем многообразии форм распределения наибольшее распространение в качестве теоретических получили нормальное распределение, распределение Пауссона, биноминальное распределение и др.
Особое место в изучении вариации принадлежит нормальному закону, благодаря его математическим свойствам. Для нормального закона выполняется правило трех сигм, по которому вариация индивидуальных значений признака находится в пределах от величины средней. При этом в границах находится около 70% всех единиц, а в пределах — 95%.
Оценка соответствия эмпирического и теоретического распределений производится с помощью критериев согласия, среди которых широко известны критерии Пирсона, Романовского, Ястремского, Колмогорова.