Имитационные модели реальных систем, или Что такое моделирование?

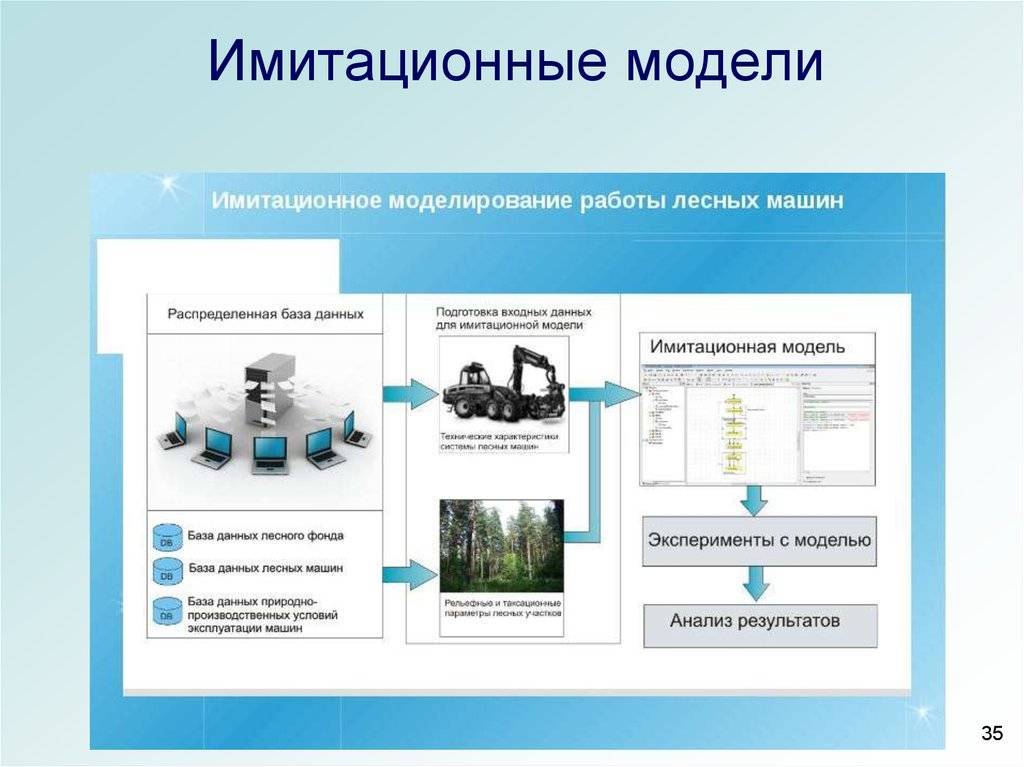
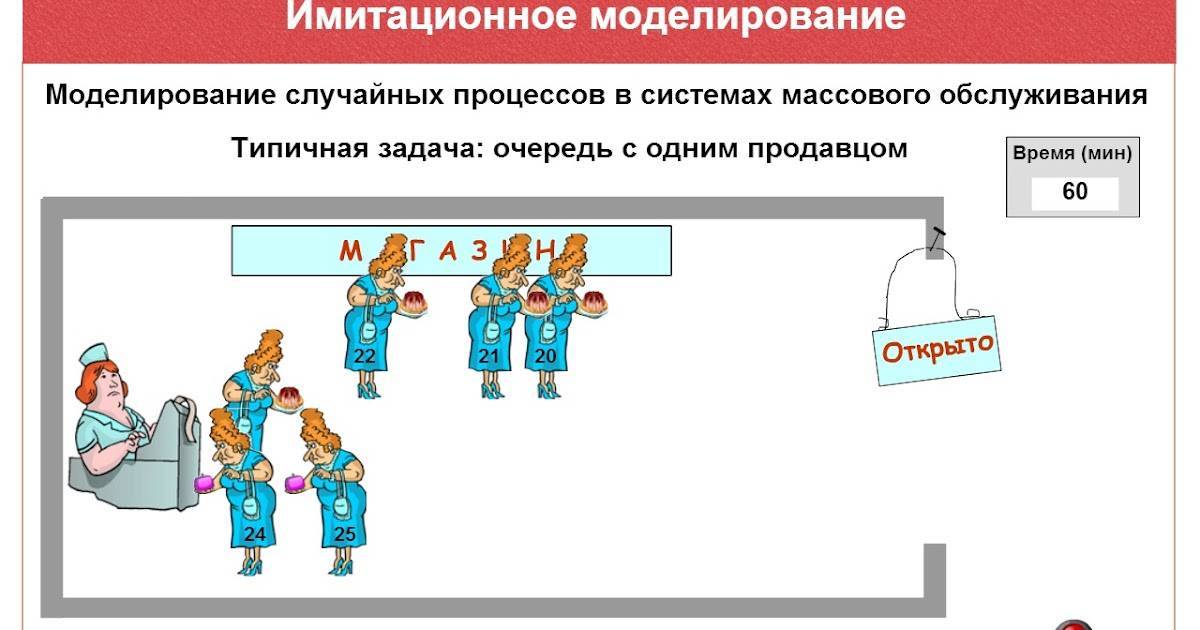
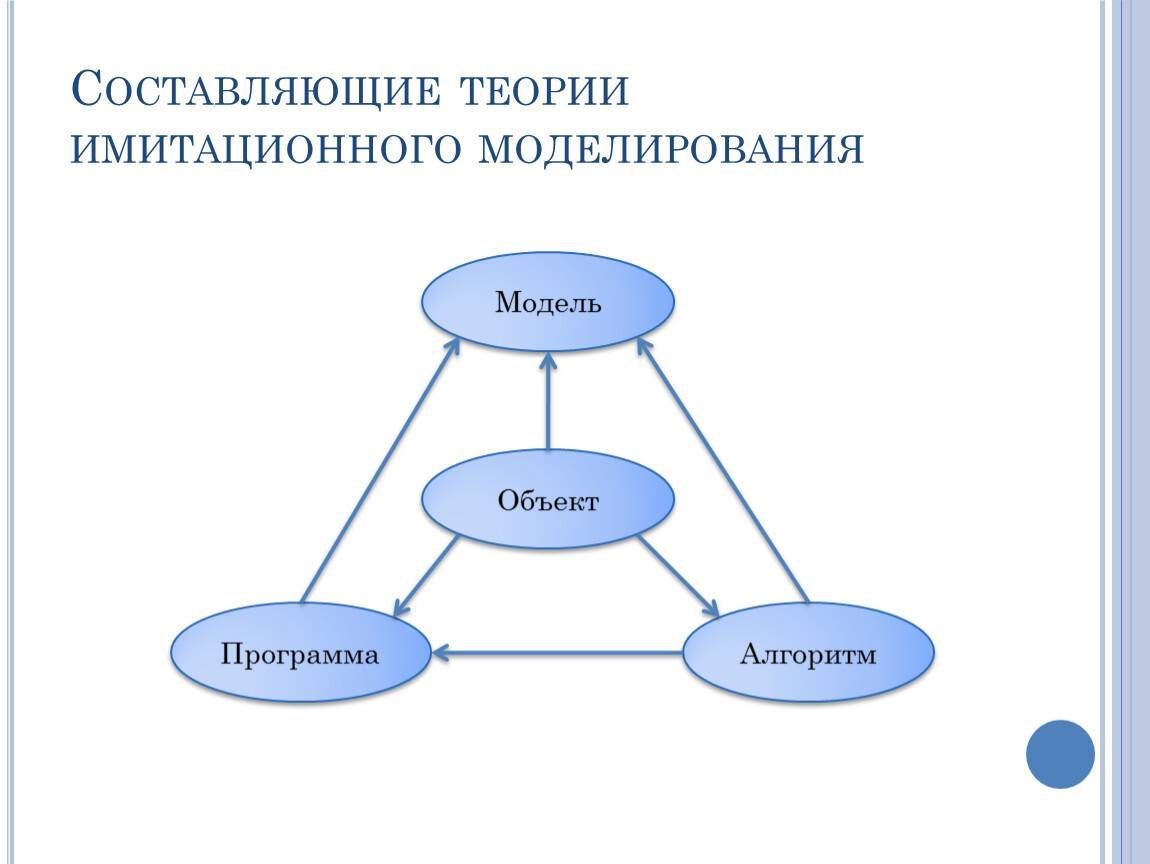
Зачем нужны имитационные модели

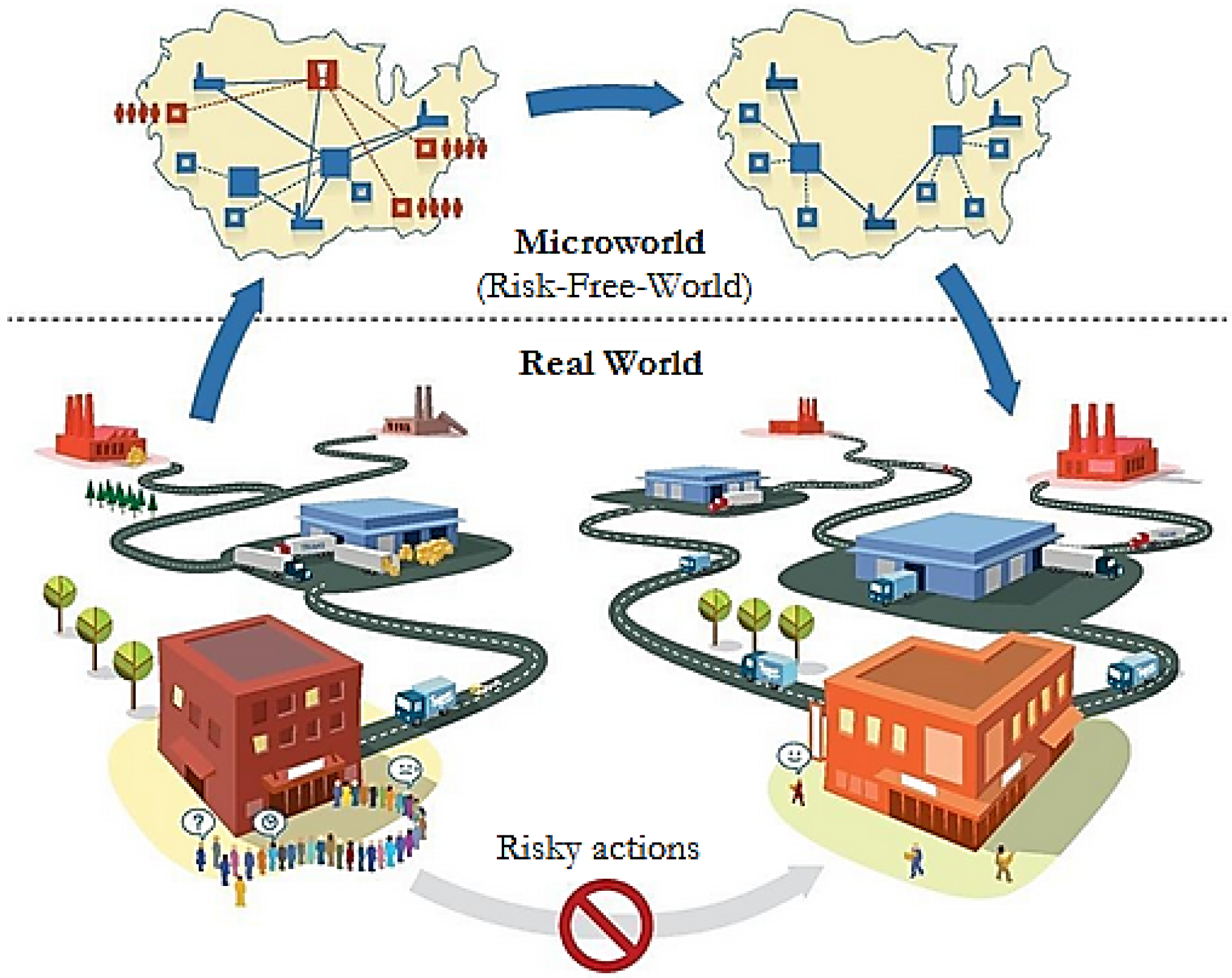
Чтобы программа могла учиться на собственном опыте, ей нужна среда, в которой можно было бы проверять идеи и получать знания из собственных ошибок и достижений. Такая среда может быть реальной (например, на частных дорогах, в ограниченном воздушном пространстве, либо на учебной конвейерной линии) или виртуальной.

Хотя тренировочные среды из реального мира больше похожи на действительность, они имеют много недостатков. Создание реальных сред для экспериментов затратно, а в некоторых случаях такие среды могут представлять риск для людей и окружающей среды. Иногда подобные эксперименты могут быть ограничены законодательно.

Имитационные модели не имеют таких ограничений – они дёшевы, и их можно гибко настраивать под конкретные нужды. Кроме того, модели в виртуальных средах могут воспроизводить процессы быстрее, чем они происходили бы в реальности, что экономит время. Примером стала разгромная победа модели системы от OpenAI над чемпионами мира в стратегической игре Dota 2. За десять месяцев обучения система OpenAI получила опыт, соответствующий 45 000 человеко-лет.

Глубокое обучение с подкреплением – это всё ещё новое направление в мире искусственного интеллекта, и пока оно находится в стадии развития. В то же время имитационное моделирование в течение десятилетий регулярно используется в практике, и существует огромное количество примеров применения технологии в бизнесе.

Специалисты по имитационному моделированию обычно работают так: создаётся имитационная модель, затем с ней проводятся эксперименты (оптимизация, эксперименты Монте-Карло, варьирование параметров и т. д.), а результаты используются для принятия решений в моделируемой бизнес-системе. Такой подход требует участия человека, который проводит эксперименты с моделью и получает от нее информацию.

При машинном обучении алгоритмы (т.н. обучающиеся агенты) способны самостоятельно извлекать подходящие линии поведения и стратегии из имитируемых систем. Логичное решение – заставить алгоритмы учиться на имитационных моделях. С учётом того, что исследователи в области ИИ переходят от игр к бизнес-задачам, это особенно актуально.

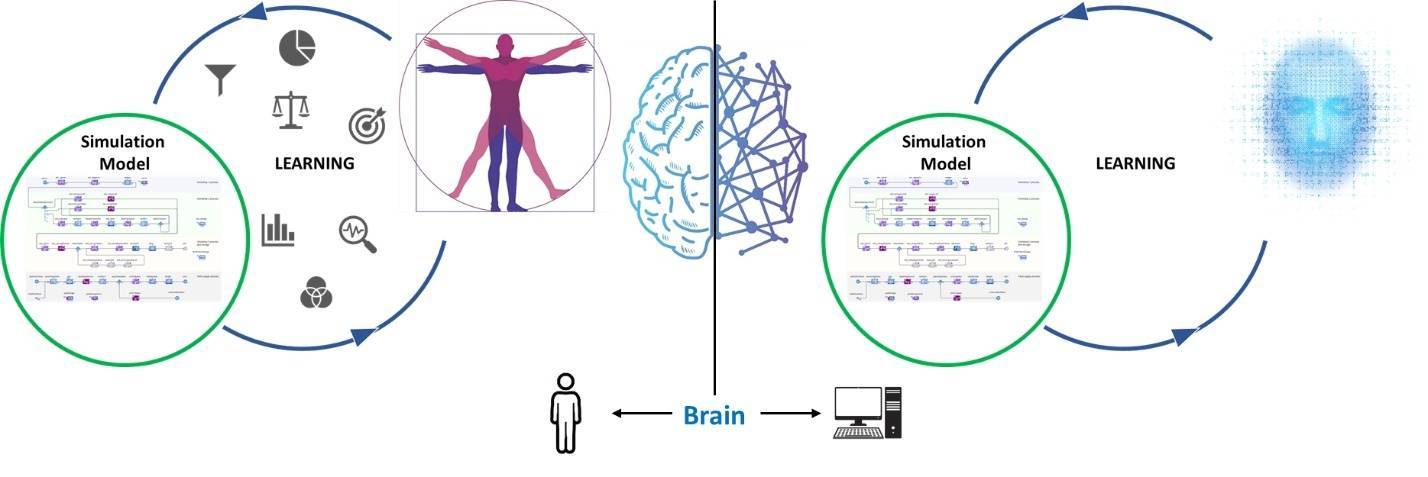
Как машинное обучение работает с имитационным моделированием

Аналитический способ представления задачи 1

Аналитический явный способ

Эта модель весьма далека от реальности. Что-либо изучить на ней представляется
проблематичным, так как из неё можно найти только время
T
и место встречи
S.
Идеализация заключается в том, что дорога считается идеально прямой, без
уклонов и подъёмов, скорости объектов считаются постоянными, желания объектов
не меняются, силы безграничны, отсутствуют помехи для движения, модель не
зависит от величин
D,
V₁,
V₂
(они могут быть сколь угодно большими или малыми).

T1 := D/(V1 + V2) S1 := V1 · T1

Реальность обычно не имеет ничего общего с такой постановкой задачи. Но за счёт
большой идеализации (идеализации большого порядка) получается очень простая
модель, которая может быть разрешена в общем виде (аналитически)
математическими способами. Так формулируются чаще всего алгоритмические модели,
где протянута цепочка вычислений от исходных данных к выходу. Поэтому мы
применили в записи знак присваивания
(:=).
После вычисления правой части выражения её значение присваивается переменной,
стоящей в левой части. Далее значение этой переменной применено в правой части
следующего выражения. Схематически это выглядит так, как показано
на
рис. 1.18.

Рис. 1.18. Схема решения задачи о встрече(аналитический явный способ)

Аналитический неявный способ

В данной формулировке за счёт использования знака уравнивания получена связь
переменных
f(T, V₁, V₂, D, S) = 0
в виде системы уравнений. Устанавливая знак «?» на различные
переменные, можно формулировать при необходимости целый ряд произвольных задач,
например так:

T1 · (V1 + V2) = D S1 = V1 · T1 T1 = ?

При этом задачи формулируются пользователем и не предусматриваются специально
моделировщиком. То есть модель имеет вид объекта. Мы получили более
качественную модель. Идеализация её велика, но за счёт неявной формы записи
появилась возможность изменения задачи, изучения на ней целого ряда проблем.

Этапы

Сейчас рассмотрим основные этапы разработки имитационной модели. Они включают её формулировку в самом начале процесса, построение концептуальной модели, выбор способа моделирования, выбор аппарата моделирования, планирование, выполнение задачи. На последнем этапе происходит анализ и обработка всех полученных данных. Построение имитационной модели – это сложный и длительный процесс, который требует большого внимания и понимания сути дела. Заметьте, что сами этапы занимают максимум времени, а процесс моделирования на компьютере – не больше нескольких минут

Очень важно использовать правильные модели имитационного моделирования, так как без этого не получится добиться нужных результатов. Какие-то данные получены будут, но они будут не реалистичны и не продуктивны

Подводя итоги статьи, хочется сказать, что это очень важная и современная отрасль

Мы рассмотрели примеры имитационных моделей, чтобы понять важность всех этих моментов. В современном мире моделирование играет огромную роль, так как на его основании развиваются экономика, градостроение, производство и так далее

Важно понимать, что модели имитационных систем очень востребованы, так как они невероятно выгодны и удобны. Даже при создании реальных условий не всегда можно получить достоверные результаты, так как всегда влияет множество схоластических факторов, которые учесть просто невозможно.

Виды

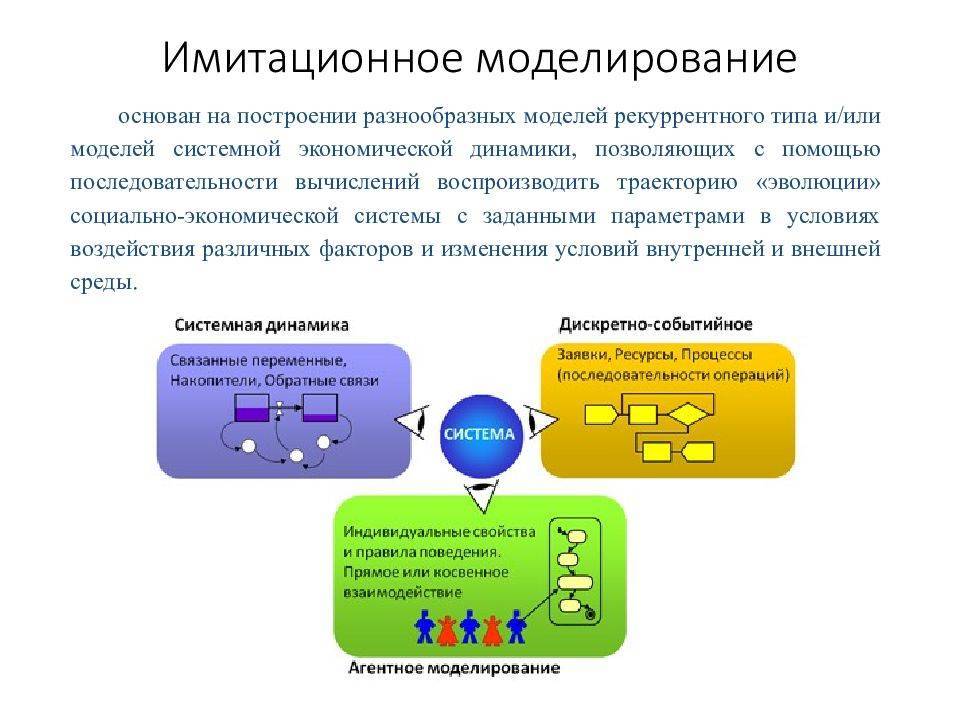
Имитационные модели исследования могут быть нескольких видов. Так, рассмотрим подходы имитационного моделирования. Первое – это системная динамика, которая выражается в том, что есть связанные между собой переменные, определенные накопители и обратная связь. Таким образом чаще всего рассматриваются две системы, в которых есть некоторые общие характеристики и точки пересечения. Следующий вид моделирования – дискретно-событийное. Оно касается тех случаев, когда есть определенные процессы и ресурсы, а также последовательность действий. Чаще всего таким способом исследуют возможность того или иного события через призму ряда возможных или случайных факторов. Третий вид моделирования – агентный. Он заключается в том, что изучаются индивидуальные свойства организма в их системе. При этом необходимо косвенное или прямое взаимодействие наблюдаемого объекта и других.

Дискретно-событийное моделирование предлагает абстрагироваться от непрерывности событий и рассматривать только основные моменты. Таким образом случайные и лишние факторы исключаются. Этот метод максимально развит, и он используется во множестве сфер: от логистики до производственных систем. Именно он лучше всего подходит для моделирования производственных процессов. Кстати, его создал в 1960-х годах Джеффри Гордон. Системная динамика – это парадигма моделирования, где для исследования необходимо графическое изображение связей и взаимных влияний одних параметров на другие. При этом учитывается фактор времени. Только на основе всех данных создается глобальная модель на компьютере. Именно этот вид позволяет очень глубоко понять суть исследуемого события и выявить какие-то причины и связи. Благодаря этому моделированию строят бизнес-стратегии, модели производства, развитие болезней, планирование города и так далее. Этот метод был изобретён в 1950-х годах Форрестером.

Агентное моделирование появилось в 1990-х годах, оно является сравнительно новым. Это направление используется для анализа децентрализованных систем, динамика которых при этом определяется не общепринятыми законами и правилами, а индивидуальной активностью определенных элементов. Суть этого моделирования заключается в том, чтобы получить представление о новых правилах, в целом охарактеризовать систему и найти связь между индивидуальными составляющими

При этом изучается элемент, который активен и автономен, может принимать решения самостоятельно и взаимодействовать со своим окружением, а также самостоятельно меняться, что очень важно

Моделирование и эксперимент

Иногда имитационные исследования проводятся в экспериментальных условиях. Связь между моделированием и экспериментом уходит своими корнями очень далеко. Однако на смену не всегда безопасным экспериментам пришло моделирование, которое будет успешным в том случае, если при имитации сложного явления в наличии имеется огромное количество информации об этом явлении. Такие переменные, как температура, давление, влажность, скорость ветра, оцениваются тысячами точек на суперкомпьютере, таким образом можно показать имитацию развития шторма. Эта дисциплина набирает все большую популярность как в общественной жизни, так и в промышленности, так как может помочь в проектировании, создании и оценке сложных систем. Дизайнеры, программисты, аналитики, инженеры так или иначе используют элементы компьютерного имитационного моделирования. Преимуществами моделирования являются получение более глубокое понимания процесса, выявление проблемных зон, оценка эффективности системы или процессов.

Компьютерное моделирование – это дисциплина конструирования модели реальной или теоретической физической системы, которая воплощает в себе принцип «обучение через действие». Использование моделирования является деятельностью, которая является столь же естественной, как ребенок, который играет с игрушками. Дети учатся понимать окружающий мир путем имитации. Чтобы лучше понять реальность и все ее сложности, мы должны создавать искусственные объекты и динамично отыгрывать с ними роли.

Разработка имитационной модели

Она заключается в том, что каждый объект имеет определенный набор своих характеристик. Все они хранятся в компьютере при помощи специальных таблиц. Взаимодействие значений и показателей всегда описывается при помощи алгоритма.

Особенность и прелесть моделирования в том, что каждый его этап постепенный и плавный, что дает возможность пошагово менять характеристики и параметры и получать разные результаты. Программа, в которой задействованы имитационные модели, выводит информацию о полученных результатах, опираясь на те или иные изменения. Часто используется графическое или анимированное их представление, сильно упрощающее восприятие и понимание многих сложных процессов, которые осознать в алгоритмичном виде довольно сложно.

Полезное дополнение к математическим моделям

Математическая модель – это абстрактная модель, которая использует математический язык для описания поведения системы. Она применяется в области естественных наук и инженерных дисциплин, а также в социальных науках (экономика, социология и политология). Математическое моделирование – метод моделирования реальных ситуаций с помощью математических уравнений для прогнозирования их будущего поведения. Оно использует такие инструменты, как решения, теории, теория массового обслуживания, линейное программирование, и требует большого количества работы с числами.

Традиционным считается формальное моделирование систем с помощью математической модели, которая пытается найти аналитические решения для некоторых проблем, она позволяет прогнозировать поведение системы при помощи набора параметров и начальных условий. Компьютерное моделирование – это программа, которая пытается имитировать абстрактные модели конкретной системы. Оно стало полезной частью математического моделирования многих природных систем в физике, химии и биологии, антропогенных систем в экономике, психологии и социальных науках и в процессе проектирования новых технологий, и все это для того, чтобы получить представление о работе этих систем.

Компьютерные симуляторы

Компьютерные симуляторы используются для изучения динамического поведения объектов или систем в ответ на условия, которые не могут легко или безопасно применяться в реальной жизни. Например, ядерный взрыв может быть описан с помощью математической модели, включающей такие переменные, как температура, скорость и количество радиоактивных выбросов. Дополнительные математические уравнения могут быть использованы для корректировки модели с изменением отдельных переменных, таких как количество расщепляющегося материала, который произвел взрыв. Симуляция реального процесса помогает безопасно измерить и предсказать, как на функционирование всей системы может повлиять изменение отдельных ее компонентов.

Случайные процессы

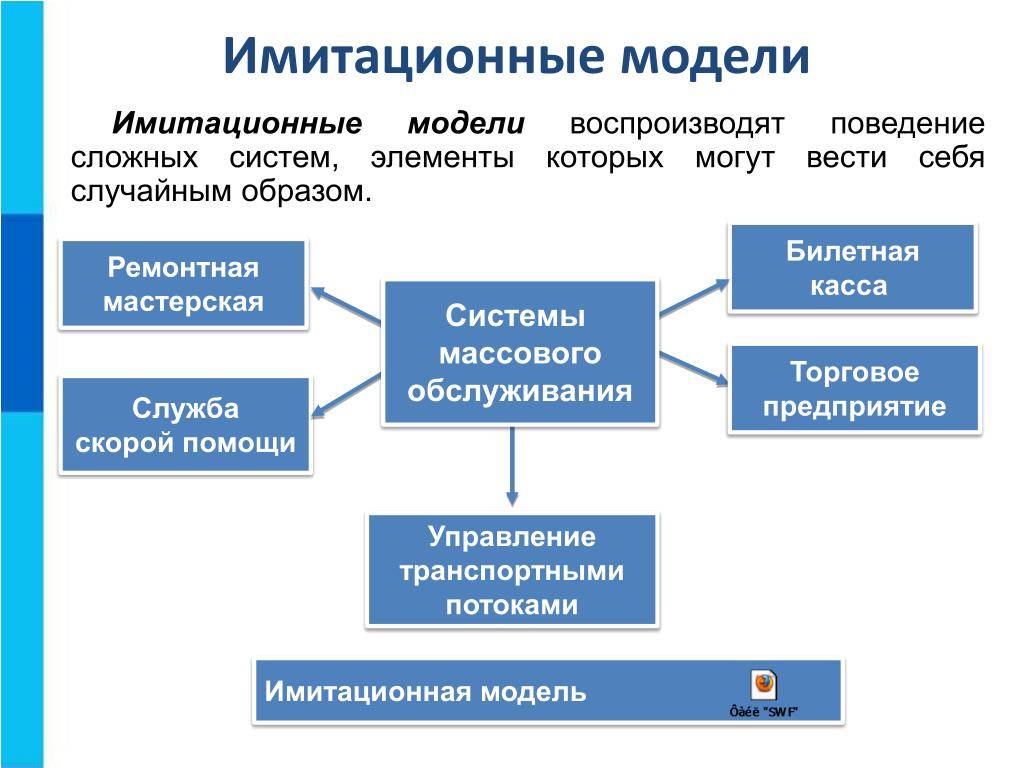
Наименование очень просто понять, если провести параллель из обычной жизни. Например, когда вы стоите в очереди в магазине, который закрывается через 5 минут, и гадаете, успеете ли вы приобрести товар. Также проявление случайности можно заметить, когда вы звоните кому-то и считаете гудки, думая, с какой вероятностью дозвонитесь. Возможно, кому-то это покажется удивительным, но именно благодаря таким простым примерам в начале прошлого века зародилась новейшая отрасль математики, а именно теория массового обслуживания. Она использует статистику и теорию вероятности для того, чтобы сделать некоторые выводы. Позже исследователи доказали, что эта теория очень тесно связана с военным делом, экономикой, производством, экологией, биологией и т. д.

Применение имитационного моделирования[]

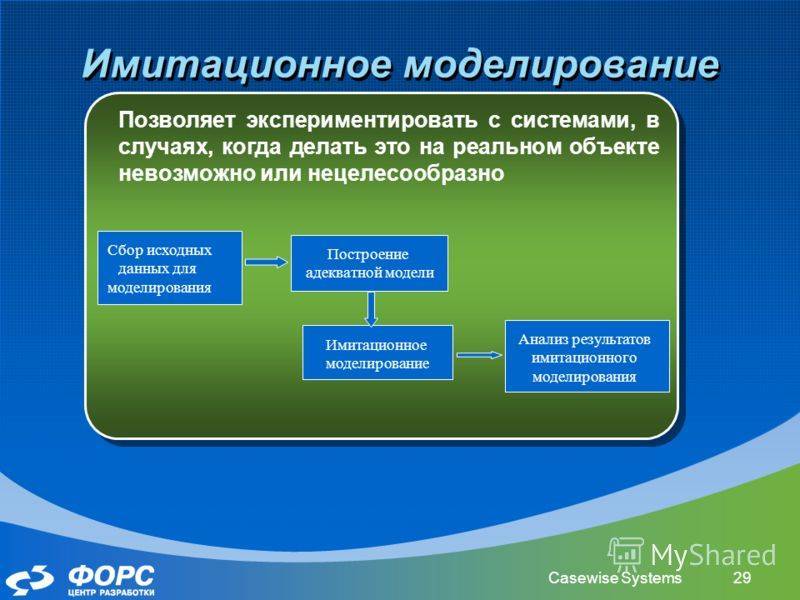
К имитационному моделированию прибегают, когда :

– дорого или невозможно экспериментировать на реальном объекте;

– невозможно построить аналитическую модель: в системе есть время, причинные связи, последствие, нелинейности, стохастические (случайные) переменные;

– необходимо сымитировать поведение системы во времени.

Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между ее элементами или другими словами — разработке симулятора исследуемой предметной области для проведения различных экспериментов.

Имитационное моделирование позволяет имитировать поведение системы во времени. Причём плюсом является то, что временем в модели можно управлять: замедлять в случае с быстропротекающими процессами и ускорять для моделирования систем с медленной изменчивостью. Можно имитировать поведение тех объектов, реальные эксперименты с которыми дороги, невозможны или опасны. С наступлением эпохи персональных компьютеров производство сложных и уникальных изделий, как правило, сопровождается компьютерным трёхмерным имитационным моделированием.             Эта точная и относительно быстрая технология позволяет накопить все необходимые знания, оборудование и полуфабрикаты для будущего изделия до начала производства. Компьютерное 3D моделирование теперь не редкость даже для небольших компаний.

Виды и цели моделирования в информатике

• учебное моделирование — это процесс, который необходим для обучения студентов, учеников и других обучающихся людей;
• моделирование для опытов — это процесс, при котором необходимо выяснить влияние на реальный объект каких-либо изменений в его сущность;
• имитационное моделирование — это процесс, при котором происходит имитация реального объекта с максимальным количеством его свойств для предугадывания исхода какого-либо события с объектом;
• игровое моделирование — это моделирование объектов для их использования в игровой индустрии;
• научно-техническое моделирование — это процесс, который применяется в различных научных исследованиях.

Моделирование помогает:

• проектировать новые реальные объекты, на основе уже имеющихся моделей (проектировать новые автомобили); 
• проводить расчеты последствий после внесения изменений в реальные объекты (что будет, если пересадить автомобиль на атомное топливо);
• обеспечить подтверждение эффективности принятых решений (электромобили лучше дизельных автомобилей);
• представлять материальные предметы (проект жилого дома);
•  и др.

Моделирование в информатике не происходит просто так, оно всегда преследует цель решить какую-то поставленную задачу. Задачи, которые решает моделирование, делятся на 2 большие группы:

1. Прямые задачи. Это задачи, в которых задаются точные исходные данные и условия, и они требуют конкретного ответа. Например, такой задачей будет поиск ответа на вопрос: «Что будет, если мы сделаем так-то и так-то?». Результатом такой задачи будет один ответ или одно решение.
2. Обратные задачи. Это задачи без конкретных исходных данных и условий. Такими задачами будет поиск ответа на вопрос: «Как можно улучшить что-либо?». Результатом таких задач может быть множество решений.

Метод Монте-Карло

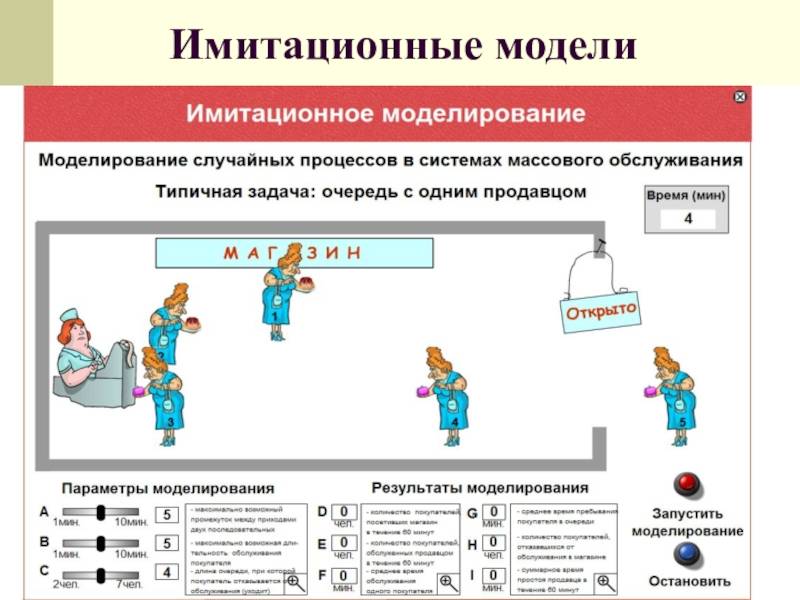
Важный метод решения задачи на самообслуживание – это метод статистических испытаний или метод Монте-Карло. Заметим, что возможности исследования случайных процессов аналитическим путем довольно сложны, а метод Монте-Карло очень прост и универсален, в чем его главная особенность. Мы можем рассмотреть пример магазина, в который заходит один покупатель или несколько, приход больных в травмпункт по одному или целой толпой и т. д. При этом мы понимаем, что всё это случайные процессы, и промежутки времени между какими-то действиями – это независимые события, которые распределяются по законам, которые можно вывести, только проведя огромное количество наблюдений. Иногда это невозможно, поэтому берется усредненный вариант. Но какова цель моделирования случайных процессов?

Дело в том, что это позволяет получить ответы на множество вопросов. Банально необходимо рассчитать, сколько человеку придется стоять в очереди при учете всех обстоятельств. Казалось бы, это довольно простой пример, но это лишь первый уровень, а подобных ситуаций может быть очень много

Иногда рассчитать время очень важно

Также можно задать вопрос о том, как можно распределить время, ожидая обслуживание. Еще более сложный вопрос касается того, как должны соотнестись параметры, чтобы до только что вошедшего покупателя очередь не дошла никогда. Кажется, что это довольно лёгкий вопрос, но если задуматься о нем и начать хотя бы немножко усложнять, становится понятно, что ответить не так легко.

Что такое моделирование с помощью компьютера?

В моделировании используется математическое описание, или модель, в виде компьютерной программы. Эта модель состоит из уравнений, которые дублируют функциональные отношения в реальной системе. Компьютерное моделирование – это использование компьютера для представления динамической реакции одной системы на поведение другой системы по образцу. Когда программа запускается, полученная математическая динамика формы аналогового поведения реальной системы и полученные результаты представляются в виде данных. Моделирование может также принять форму компьютерно-графического изображения, которое представляет динамические процессы в анимированной последовательности.

Программа для моделирования помогает представить реальный мир с помощью компьютера. Имитируя фактическое или вероятное условие, событие или ситуацию из жизни, можно найти причину события (например, аварии) или сделать прогноз будущих последствий и результатов. Моделирование может быть выполнено посредством решения систем уравнений (математическая модель), построения физической модели (масштаб), постановочной репетиции, игр или графических моделей (анимированные блок-схемы). А симуляторы – это очень полезные инструменты, которые позволяют проводить эксперименты без риска.

Моделирование в информатике: этапы

• манекен — это модель человеческой фигуры;
• глобус — это модель нашей планеты;
• и т. д.

О физическом моделировании мы поговорим в другой раз, а сегодня нас интересуют этапы, через которые проходит моделирование в информатике с применением электронно-вычислительных машин.

Этапы создания моделей  в информатике:

• вербальная или задокументированная постановка задачи в виде технического задания модели;
• математический анализ поставленной задачи с целью выяснения необходимых подходов и инструментов для моделирования;
• разработка модели или сам процесс моделирования с использованием компьютера;
• использование модели для поставленных задач;
• получение  необходимого результата.

Пример модели: имитация + обучение с подкреплением

Машинное обучение против алгоритмов оптимизации на примере светофора. Управление с помощью обучения с подкреплением – справа.

Данный пример модели был заменен. Теперь вы можете посмотреть другие модели от наших партнеров:

• Project Bonsai от Microsoft;
• примеры автоматического машинного обучения от h2o.ai;
• примеры оптимизации работы имитационных моделей с помощью ИИ от Pathmind.

Большое спасибо команде Skymind, в частности, Сэмюэлю Одету и Эдуардо Гонсалесу, за их участие в этом проекте; их вклад был неоценим. Если у вас возникли вопросы о библиотеке DL4J, использованной в модели, то их можно задать на странице команды в Gitter.

Другие материалы о том, как ИМ используется вместе с ИИ:

• Общая информация: Имитационная платформа для обучения и тестирования ИИ для бизнес-приложений
• Видео: Имитационные модели – виртуальная среда для обучения и тестирования ИИ для бизнес-приложений
• Аналитическая статья (на англ.): ИИ и имитационное моделирование для бизнеса

• Блог: Искусственный интеллект и имитационное моделирование

• Блог: Что общего у ИМ, машинного обучения и глубокого обучения?

• Видео: ИМ и обучение с подкреплением – мнение экспертов
• Видео вебинара: Тренировка алгоритмов ИИ с помощью ИМ и глубокого обучения
• Видео вебинара от Skymind и AnyLogic: ИМ и автоматическое машинное обучение

Адекватность модели

Поскольку модель является выражением конечного ряда и только важнейших для
конкретного исследования аспектов сущности, то она не может быть абсолютно
идентичной моделируемому объекту. Кроме этого, реальный объект бесконечен для
познания. Поэтому нет смысла стремиться к бесконечной точности при построении
модели. Для выяснения необходимой степени адекватности обычно строят ряд
моделей, начиная с грубых, простых моделей и двигаясь ко все более сложным и
точным. Как только затраты на построение очередной модели начинают превышать
планируемую отдачу от модели, то уточнение модели прекращают. Первоначальные
шаги производятся в каком-либо существующем универсальном моделирующем пакете.
После одобрения модели под неё пишется специализированный пакет. Необходимость
в этом возникает в случае, если функционирование модели в универсальной среде
моделирования не удовлетворяет требованиям быстродействия (или каким-то другим).

В задачи данного курса входит изучение приёмов и способов, необходимых для
формализации, изучения и интерпретации систем.

Моделирование прикладная инженерная наука класса технологических.
Моделирование дисциплина, ставящая целью построение моделей и их
исследование посредством собственных универсальных методов, а также
специфических методов смежных с ней наук (математика, исследование операций,
программирование).

Основные определения[]

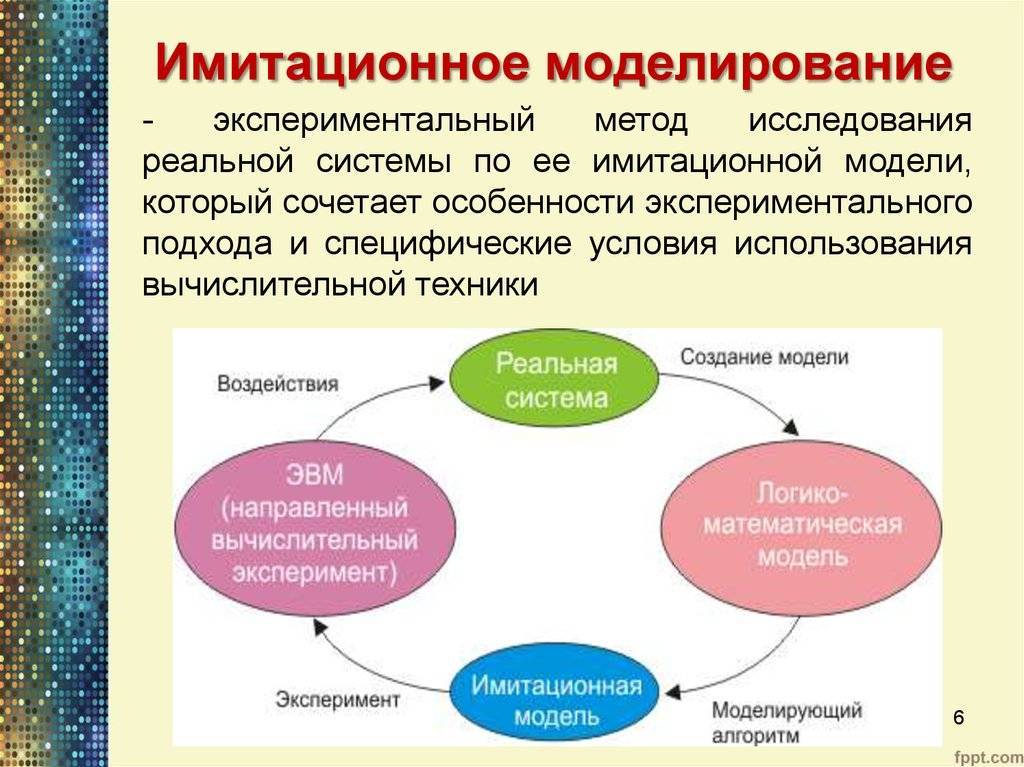
Имитационное моделирование (ситуационное моделирование) — метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику.

Имитационное моделирование — это метод исследования, при котором изучаемая система заменяется моделью, с достаточной точностью описывающей реальную систему, с которой проводятся эксперименты с целью получения информации об этой системе. Экспериментирование с моделью называют имитацией (имитация — это постижение сути явления, не прибегая к экспериментам на реальном объекте).

Имитационное моделирование — это частный случай математического моделирования. Существует класс объектов, для которых по различным причинам не разработаны аналитические модели, либо не разработаны методы решения полученной модели. В этом случае аналитическая модель заменяется имитатором или имитационной моделью.

Имитационным моделированием иногда называют получение частных численных решений сформулированной задачи на основе аналитических решений или с помощью численных методов.

Имитационная модель — логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта.

Образование

Анализу имитационных моделей в школах уделяется мало внимания. К сожалению, это может отразиться на будущем довольно серьезно. Дети должны со школы знать некоторые базовые принципы моделирования, так как развитие современного мира без этого процесса невозможно. В базовом курсе информатики дети могут с легкостью использовать имитационную модель “Жизнь”.

Более основательное изучение может преподаваться в старших классах или в профильных школах. Прежде всего надо заняться изучением имитационного моделирования случайных процессов

Помните, что в российских школах такое понятие и методы только начинают вводиться, поэтому очень важно держать уровень образования учителей, которые со стопроцентной гарантией столкнутся с рядом вопросов от детей

При этом не будем усложнять задачу, акцентируя внимание на том, что речь идет об элементарном введении в эту тему, которое можно подробно рассмотреть за 2 часа

После того как дети усвоили теоретическую базу, стоит осветить технические вопросы, которые касаются генерации последовательности случайных чисел на компьютере. При этом не надо загружать детей информацией о том, как работает вычислительная машина и на каких принципах строится аналитика. Из практических навыков их нужно учить создавать генераторы равномерных случайных чисел на отрезке или случайных чисел по закону распределения.

Детерминированность

Имитационные математические модели строятся на том, что они копируют качества и характеристики неких реальных систем. Рассмотрим пример, когда необходимо исследовать количество и динамику численности определённых организмов. Для этого при помощи моделирования можно отдельно рассматривать каждый организм, чтобы анализировать конкретно его показатели. При этом условия чаще всего задаются вербально. К примеру, по истечении какого-то отрезка времени можно задать размножение организма, а по прошествии более длительного срока – его гибель. Выполнение всех этих условий возможно в имитационной модели.

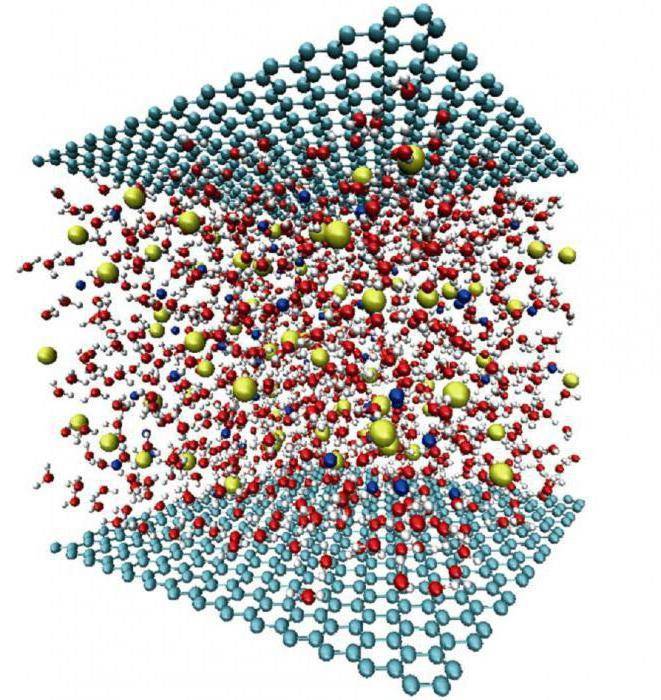
Очень часто приводят примеры моделирования движения молекул газа, ведь известно, что они двигаются хаотично. Можно изучать взаимодействие молекул со стенками сосуда или друг с другом и описывать результаты в виде алгоритма. Это позволит получать усредненные характеристики всей системы и выполнять анализ. При этом надо понимать, что подобный компьютерный эксперимент, по сути, можно назвать реальным, так как все характеристики моделируются очень точно. Но в чём смысл этого процесса?

Дело в том, что имитационная модель позволяет выделить конкретные и чистые характеристики и показатели. Она как бы избавляется от случайных, лишних и ещё ряда других факторов, о которых исследователи могут даже не догадываться. Заметим, что очень часто детерминирование и математическое моделирование схожи, если в качестве результата не должна быть создана автономная стратегия действий. Примеры, которые мы выше рассмотрели, касаются детерминированных систем. Они отличаются тем, что у них нет элементов вероятности.