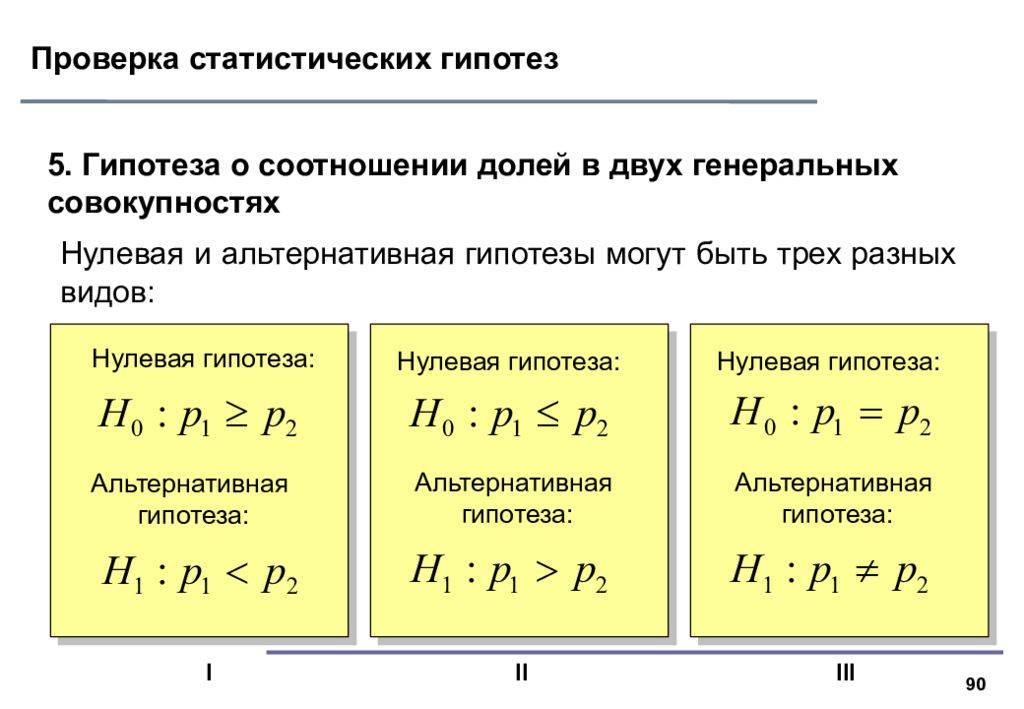
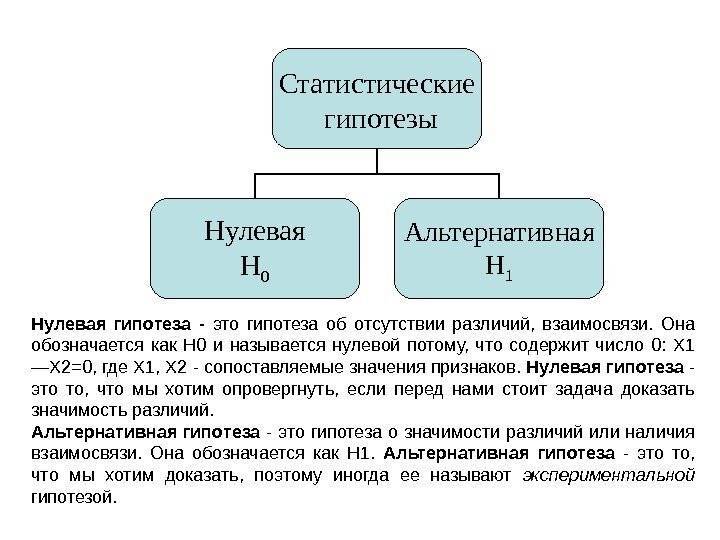
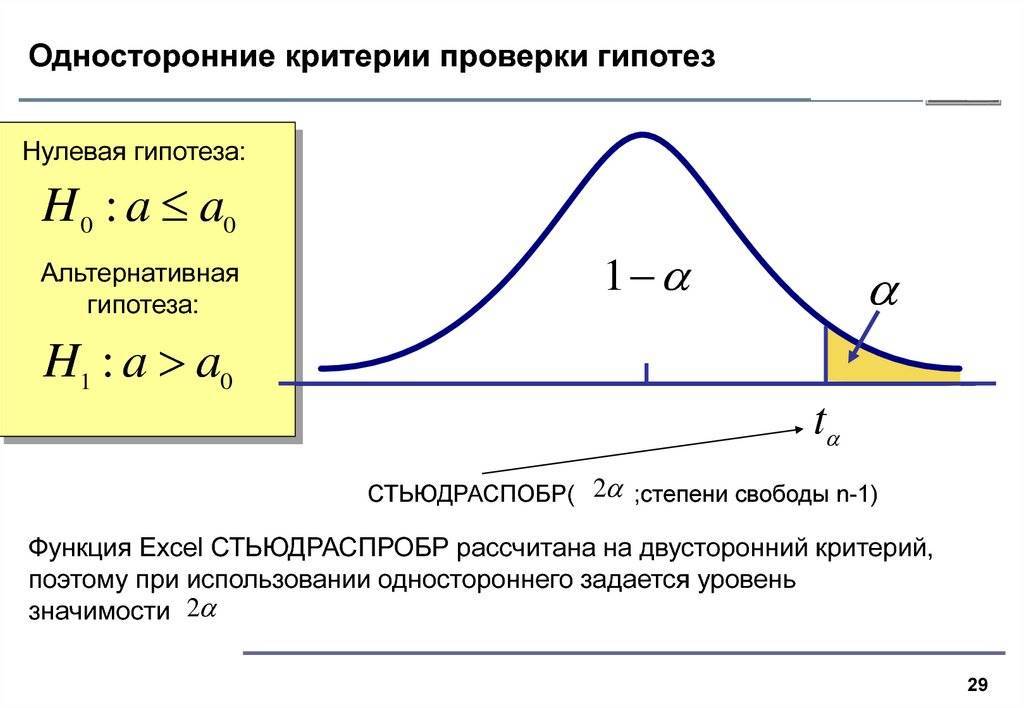
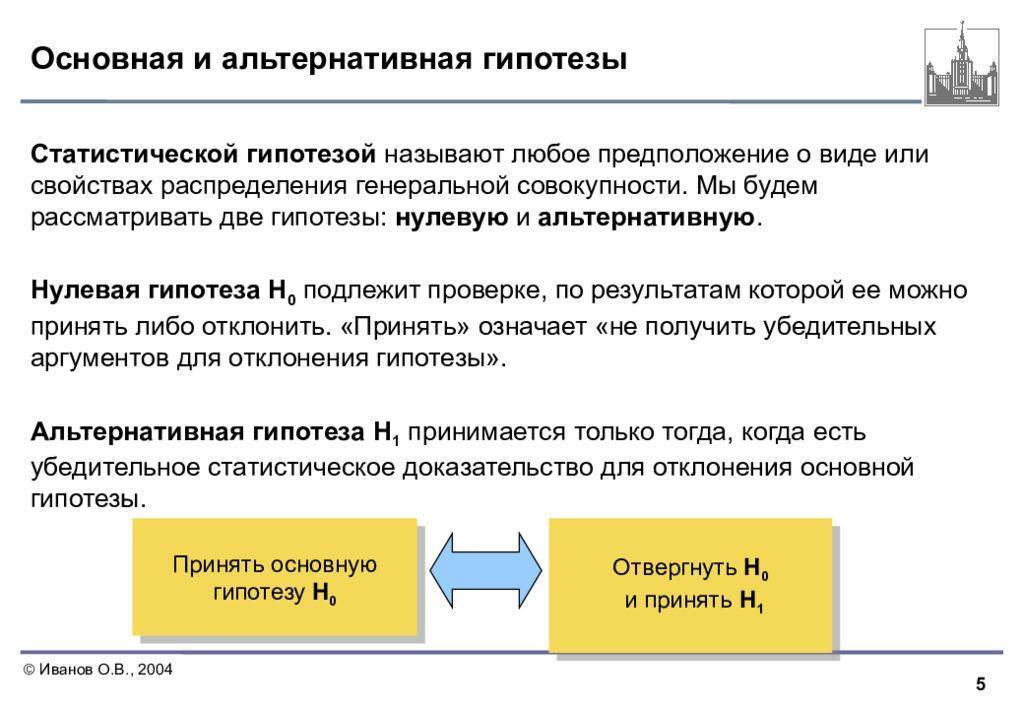
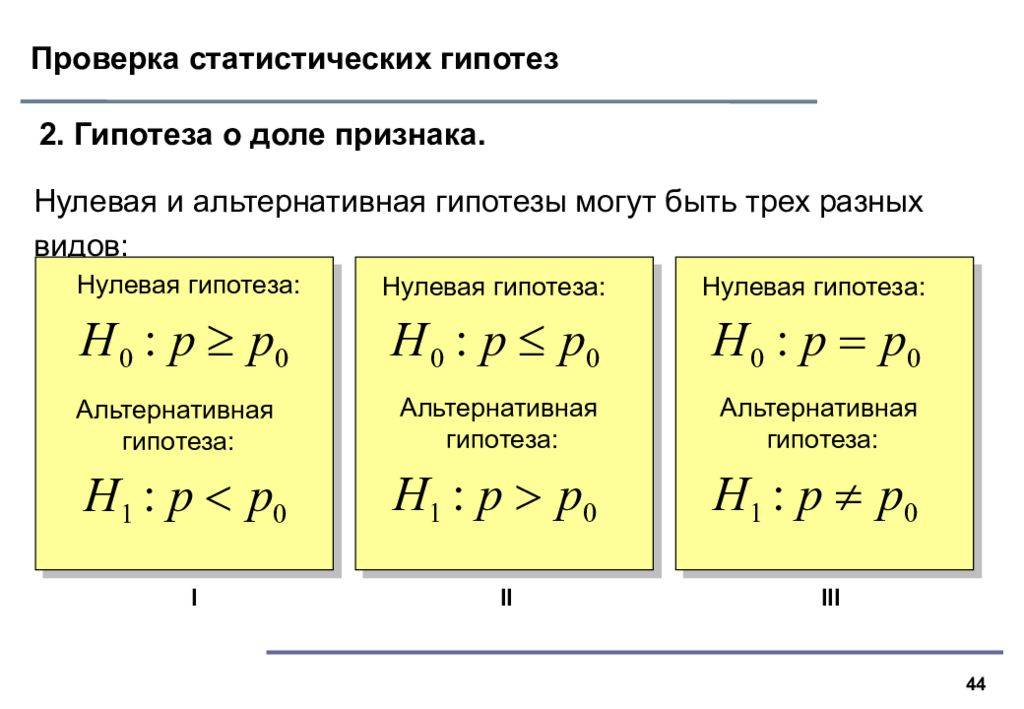
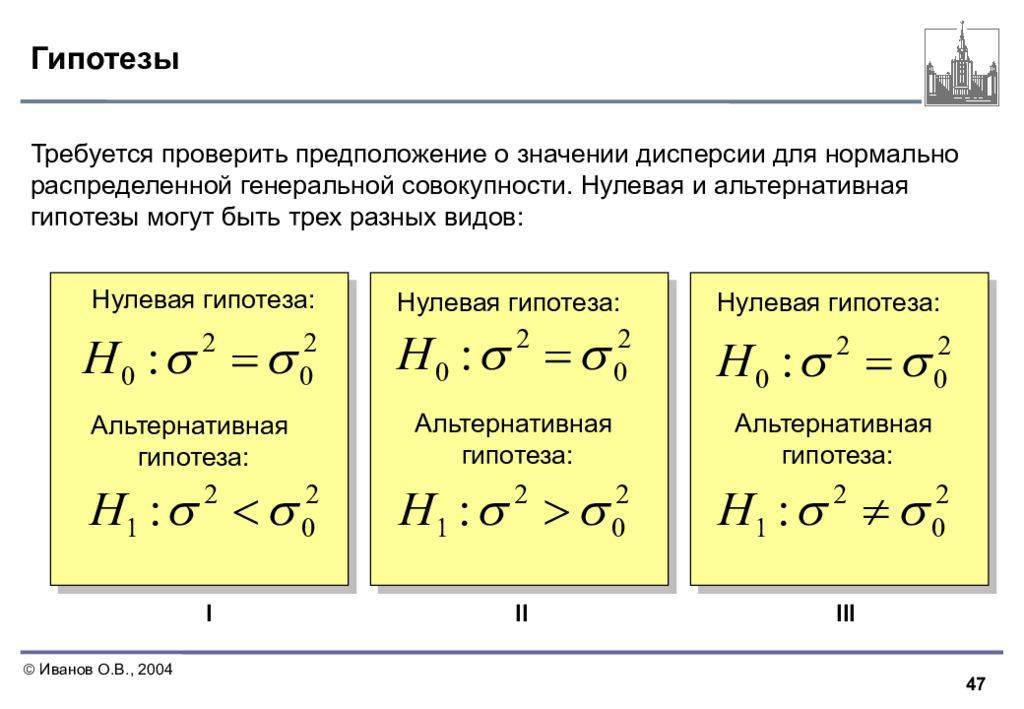
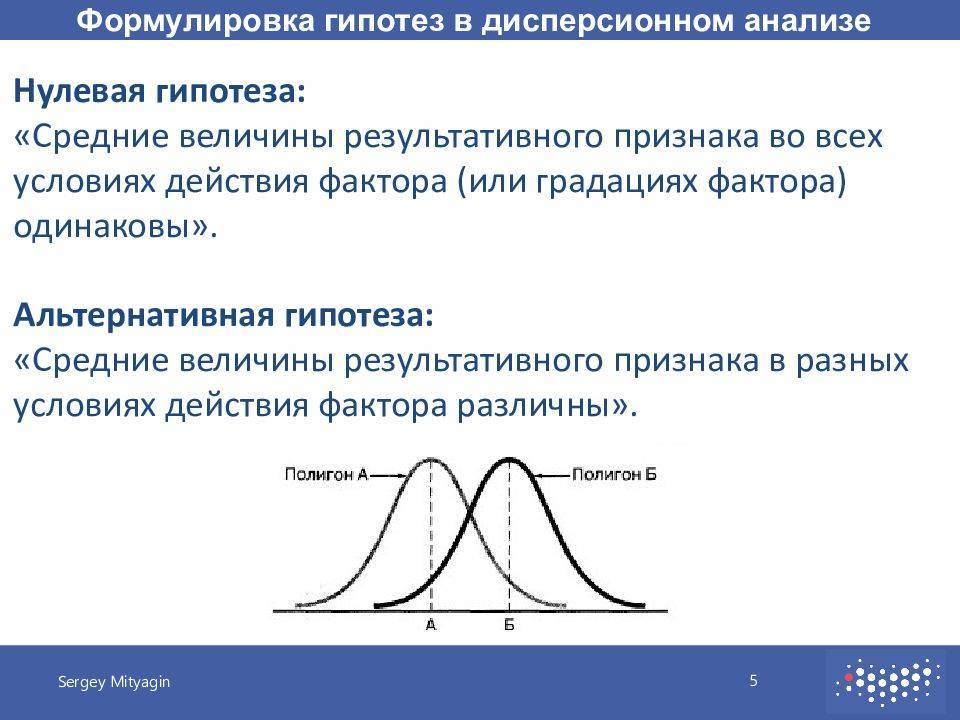
Что это и кому это нужно?
Проверка (тест) статистической гипотезы – это способ математического определения верности некоторого утверждения на основе
закона распределения. Освоив этот метод, Вы сможете делать математически обоснованные выводы, например:
Пример #1
Вы изготавливаете кубики для игры в кости и чтобы убедиться, что кубик отлично сбалансирован, Вы проводите тест – бросаете кости 600 раз
и решаете, что если каждое число выпало 100±10 раз, то кубик сбалансирован.
Пример #2
На производстве 5% продукции отбраковывается, Вы разработали новую технологию и хотите проверить, уменьшится ли
количество брака.
4.3 Понятие гипотезы в педагогике
Гипотеза
исследования –
методологическая характеристика
исследования, научное предположение,
выдвигаемой для объяснения какого-либо
явления и требующее проверки на опыте для
того, чтобы стать достоверным научным
знанием. От простого предположения
гипотеза отличается рядом признаков. К ним
относят:
– соответствие
фактам, на основе которых и для обоснования
которых она создана
– проверяемость
– приложимость к
возможно более широкому кругу явлений
– относительная
простота.
В гипотезе
органически сливаются два момента:
выдвижение некоторого положения и
последующее логическое и практическое
доказательство.
Педагогическая
гипотеза (научное предположение о
преимуществе того или иного метода) в
процессе статистического анализа
переводится на язык статистической науки
и заново формулируется, по меньшей мере, в
виде двух статистических гипотез.
Возможны два
типа гипотез: первый тип — описательныегипотезы, в которых описываются причины и
возможные следствия. Второй тип — объяснительныев них дается объяснение возможным
следствиям из определенных причин, а также
характеризуются условия, при которых эти
следствия обязательно последуют, т. е. объясняется,
в силу каких факторов и условий будет
данное следствие. Описательные гипотезы не
обладают предвидением, а объяснительные
обладают таким свойством. Объяснительные
гипотезы выводят исследователей на предположения
о существовании определенных закономерных
связеймежду
явлениями, факторами и условиями.
Гипотезы в
педагогических исследованиях могут
предполагать, что одно из средств (или
группа их) будет более эффективным, чем
другие средства. Здесьгипотетическивысказываетсяпредположение
о сравнительной эффективности средств,
способов, методов, форм обучения.
Более высокий уровень
гипотетического предсказания состоит в том,
что автор исследования высказывает
гипотезу о том, что какая-то система мер
будет не только лучше другой, ноиизрядавозможных систем она кажется
оптимальной с точки зрения определенных
критериев. Такая гипотеза нуждаетсявещеболеестрогомиоттого более развернутом
доказательстве.
Кулаичев А.П. Методы и средства анализа
данных в среде Windows. Изд. 3-е, перераб. и доп.
– М: ИнКо, 1999, стр. 129-131
Психолого-педагогический
словарь для учителей и руководителей
общеобразовательных учреждений. –
Ростов-н/ Д: Феникс, 1998, стр. 92
На
главную
На содержание
«Доверительный» способ проверки
Существует наиболее действенный способ, с помощью которого нулевая статистическая гипотеза легко проверяется на практике. Он заключается в построении диапазона значений до 95% точности.
Для начала понадобится знать формулу расчёта доверительного интервала:
X – t*Sx ≤ c ≤ X + t*Sx,
где Х — данное изначально число на основе альтернативной гипотезы;
t — табличные величины (коэффициент Стьюдента);
Sx — стандартная средняя ошибка, которая рассчитывается как Sx = σ/√n, где в числителе стандартное отклонение, а в знаменателе – объём выборки.
Итак, предположим ситуацию. До ремонта конвейер в день выпускал 32.1 кг конечной продукции, а после ремонта, как утверждает предприниматель, коэффициент полезного действия вырос, и конвейер, по недельной проверке, начал выпускать 39.6 кг в среднем.
 Нулевая гипотеза будет утверждать, что ремонт никак не повлиял на КПД конвейера. Альтернативная гипотеза скажет, что ремонт коренным образом изменил КПД конвейера, поэтому производительность его повысилась.
Нулевая гипотеза будет утверждать, что ремонт никак не повлиял на КПД конвейера. Альтернативная гипотеза скажет, что ремонт коренным образом изменил КПД конвейера, поэтому производительность его повысилась.
По таблице находим n=7, t = 2,447, откуда формула примет следующий вид:
39,6 – 2,447*4,2 ≤ с ≤ 39,6 + 2,447*4,2;
29,3 ≤ с ≤ 49,9.
Получается, что значение 32.1 входит в диапазон, а следовательно, значение, предложенное альтернативой — 39.6 — не принимается автоматически. Помните, что сначала проверяется на правильность нулевая гипотеза, а потом – противоположная.
Уровень значимости α, ошибки первого и второго рода
Уровень значимости – это вероятность ошибки
первого рода. Значение уровня значимости обычно достаточно малое и задаётся аналитиком, проверяющим гипотезу.
Чаще всего принимает значения 0,01 (1%), 0,05 (5%) и 0,1 (10%).
При проверке гипотезы всегда существует вероятность того, что будет сделано ошибочное
заключение. Существуют два рода ошибки.
Ошибка первого рода – отвержение основной гипотезы при том,
что она верна.
Ошибка второго рода – принятие основной гипотезы при том,
что она ложна.
Со значением уровня значимости связано значение уровня доверия p.
Уровень доверия p – вероятность принятия верной гипотезы. Помним: пока не
доказано, что основная гипотеза
является ложной, мы считаем её верной. Поэтому уровень значимости будет определять вероятность принятия
основной гипотезы. Если уровень значимости – вероятность отвержения
верной гипотезы, то вероятность принятия верной гипотезы: .
Аналитик сам управляет ошибкой первого рода – задаёт вероятность её наступления.
Ошибкой второго рода он управлять не может – всегда существует вероятность того, что может быть принята
неверная гипотеза. Поэтому, чтобы избежать нежелательных последствий от принятия неверной гипотезы,
основная гипотеза формулируется таким образом, чтобы риск от последствий принятия неверной гипотезы был
минимальным.
Пример 3. В лаборатории фармацевтического предприятия делается
контрольный замер на соответствие контрольного состава лекарственных препаратов стандарту. Какие
варианты гипотез могут быть предложены?
Решение.
Первый вариант.
Основная гипотеза –
лекарства соответствуют стандарту.
Альтернативная гипотеза –
лекарства не соответствуют стандарту.
Второй вариант.
Основная гипотеза –
лекарства не соответствуют стандарту.
Альтернативная гипотеза –
лекарства соответствуют стандарту.
В первом случае, принимая во внимание, что вероятность принятия основной гипотезы
высока, мы имеем высокий риск нежелательных последствий принятия неверной гипотезы. Во втором случае,
даже если мы будем вынуждены принять гипотезу, что лекарственные препараты не соответствуют стандарту,
а на самом деле имеет место ошибка второго рода, придётся провести дополнительные контрольные замеры
и более тщательно провести анализ химического состава
В любом случае, это повлечёт за собой более
тщательный анализ, а риск нежелательных последствий может оказаться не столь значимым.
По причинам, которые мы выяснили в примере 3, статистические гипотезы часто формулируются
следующим образом: “статистическая значимость между факторами незначима”, “выборки незначимо отличаются
по своим свойствам”, “фактор не имеет значимого влияния на исследуемый процесс”.
Проверка гипотезы об однородности выборок
Существует два вида гипотез об однородности выборок. Может быть
проверена однородность выборок “в слабом”: выборки однородны “в слабом”, если незначимо отличаются их
параметры, прежде всего, среднее. Может быть проверена однородность выборок “в сильном”: выборки
однородны “в сильном”, если незначимо отличаются их законы распределения.
С помощью критерия Стьюдента проверяется гипотеза об однородности выборок “в слабом”.
В этом случае основная гипотеза формулируется следующим образом: математическое ожидание первой
выборки незначимо отличается от математического ожидания второй выборки. Формально это записывается так:
.
Критерий рассчитывается по формуле:
где и
– математические ожидания первой и
второй выборок размерами и
соответственно (в качестве оценок
математических ожиданий берутся значения средних первой и второй выборок);
и
– дисперсии первой
и второй выборок;
–
число степеней свободы.
Критерий может принимать значения от минус бесконечности до плюс бесконечности. Чем
ближе значения критерия к нулю, тем больше вероятность, что основная гипотеза будет верной (при этом знак
не имеет значения).
Пусть задано значение уровня значимости
. Тогда критерий будет принимать значения в области принятия гипотезы с
вероятностью (эта вероятность называется уровнем доверия). Вероятность того,
что критерий примет значения меньшие, чем значение левой критической точки области
принятия гипотезы равна , а вероятность того, что критерий примет значение,
меньшее, чем значение правой критической точки . Значением левой критической
точки области принятия гипотезы будет являться квантиль распределения Стьюдента
уровня с df степенями свободы. Значением правой критической точки области принятия
гипотезы будет выступать квантиль распределения Стьюдента уровня с тем же
числом степеней свободы.
При проверке гипотезы об однородности выборок с помощью критерия Стьюдента
необходимо помнить, что к выборкам выдвигаются допущение, нарушение которых не
позволяет применить критерий:
- выборки должны подчиняться нормальному распределению. Если это требование
нарушается, то критерий не будет подчиняться распределению Стьюдента и,
следовательно, границы области принятия гипотезы будут найдены неверно; - в выборках не должны присутствовать резко выделяющиеся наблюдения, иначе
среднее значение будет смещено в сторону выбросов и в результате критерий даст
некорректный результат.
Пример 6. Имеются данные некоторой выборки. По ним в пакете
программных средств STATISTICA вычислены следующие показатели:
| Среднее 1-й выборки | Среднее 2-й выборки | t-критерий | Число степеней свободы | p-level |
| 19,60 | 28,21 | -1,38 | 48 | 0,17 |
Область принятия гипотезы при уровне значимости :
Сделать вывод об однородности выборок.
Ответ.
Значение t-критерия попадает в область принятия гипотезы. Может быть принята
основная гипотеза о том, что математическое ожидание первой выборки незначимо отличается от математического ожидания второй выборки. Таким образом, проверена гипотеза об однородности выборок в слабом.
С помощью критерия Колмогорова-Смирнова проверяется гипотеза об однородности выборок
“в сильном”, то есть о том, что функции распределения выборок незначимо отличаются друг от друга. За
основу критерия Колмогорова-Смирнова выступает статистика
–
максимальная по модулю разность между двумя функциями распределения выборок x и y.
Критерий рассчитывается по формуле
Границы области принятия гипотезы определяются следующим образом:
.
Если критерий принадлежит области принятия гипотезы, то при заданном уровне значимости
α нет возможности её отвергнуть, следовательно, принимается гипотеза о том, что выборки
однородны “в сильном”.
Гипотезы об однородности выборок могут быть выдвинуты как в
исследованиях поведения человека,
так и технических науках.
Пример 7. По данным некоторой выборки получены следующие показатели:
| Макс. отриц. разность | Макс. полож. разность | Значение критерия K.S. | p-level |
| -0,2 | 0,08 | 0,117 | >10 |
Область принятия гипотезы при уровне значимости :
Сделать вывод об однородности выборок.
Ответ.
Значение критерия попадает в область принятия гипотезы. Следовательно, принимается
основная гипотеза о том, что функции распределения двух выборок незначимо отличаются. Таким образом,
выборки однородны “в сильном”.
| Назад | Листать | Вперёд>>> |
Всё по теме “Математическая статистика”
Типы статистических критериев
В зависимости от проверяемой нулевой гипотезы статистические критерии делятся на группы, перечисленные ниже по разделам.
Наряду с нулевой гипотезой, которая принимается или отвергается по результату анализа выборки, статистические критерии могут опираться на дополнительные предположения, которые априори предпологаются выполненными.
Параметрические критерии предполагают, что выборка порождена распределением из заданного параметрического семейства. В частности, существует много критериев, предназначенных для анализа выборок из нормального распределения. Преимущество этих критериев в том, что они более мощные. Если выборка действительно удовлетворяет дополнительным предположениям, то параметрические критерии дают более точные результаты. Однако если выборка им не удовлетворяет, то вероятность ошибок (как I, так и II рода) может резко возрасти. Прежде чем применять такие критерии, необходимо убедиться, что выборка удовлетворяет дополнительным предположениям. Гипотезы о виде распределения проверяются с помощью критериев согласия.
Непараметрические критерии не опираются на дополнительные предположения о распределении. В частности, к этому типу критериев относится большинство ранговых критериев.
Критерии согласия
Критерии согласия проверяют, согласуется ли заданная выборка с заданным фиксированным распределением, с заданным параметрическим семейством распределений, или с другой выборкой.
- Критерий Колмогорова-Смирнова
- Критерий хи-квадрат (Пирсона)
- Критерий омега-квадрат (фон Мизеса)
Критерии сдвига
Специальный случай двухвыборочных критериев согласия.
Проверяется гипотеза сдвига, согласно которой распределения двух выборок имеют одинаковую форму и отличаются только сдвигом на константу.
- Критерий Стьюдента
- Критерий Уилкоксона-Манна-Уитни
Критерии нормальности
Критерии нормальности — это выделенный частный случай критериев согласия.
Нормально распределённые величины часто встречаются в прикладных задачах, что обусловлено действием закона больших чисел.
Если про выборки заранее известно, что они подчиняются нормальному распределению, то к ним становится возможно применять более мощные параметрические критерии.
Проверка нормальность часто выполняется на первом шаге анализа выборки, чтобы решить, использовать далее параметрические методы или непараметрические.
В справочнике А. И. Кобзаря приведена сравнительная таблица мощности для 21 критерия нормальности.
- Критерий Шапиро-Уилка
- Критерий асимметрии и эксцесса
Критерии однородности
Критерии однородности предназначены для проверки нулевой гипотезы о том, что
две выборки (или несколько) взяты из одного распределения,
либо их распределения имеют одинаковые значения математического ожидания, дисперсии, или других параметров.
Критерии симметричности
Критерии симметричности позволяют проверить симметричность распределения.
- Одновыборочный критерий Уилкоксона и его модификации: критерий Антилла-Кёрстинга-Цуккини, критерий Бхаттачария-Гаствирса-Райта
- Критерий знаков
- Коэффициент асимметрии
Критерии тренда, стационарности и случайности
Критерии тренда и случайности предназначены для проверки нулевой гипотезы об
отсутствии зависимости между выборочными данными и номером наблюдения в выборке.
Они часто применяются в анализе временных рядов, в частности, при анализе регрессионных остатков.
Уровень значимости
Вероятность возникновения ошибки первого рода называется уровнем значимости (significance level). Уровень значимости обозначают буквой $\alpha$. Поэтому ошибку первого рода иногда называют $\alpha$-ошибкой ($\alpha$-error). Обратное значение уровня значимости ($1-\alpha$) называется доверительной вероятностью или коэффициентом доверия (confidence coefficient).
Вероятность возникновения ошибки второго рода обозначают буквой $\beta$, поэтому сама ошибка называется $\beta$-ошибкой ($\beta$-error). Эта ошибка сама не используется в статистике, зато используется его обратная величина ($1-\beta$). Обратная величина $\beta$-ошибки называется мощностью критерия (power). Мощность критерия выражает вероятность правильного принятия альтернативной гипотезы.
В последнее время именно на мощность критерия больше всего обращают внимание. Потому что, исследователи и агентства не хотят тратить усилия и ресурсы на исследование области, если не будет достигнута разумная вероятность результата
Поэтому, чем больше мощность критерия, тем меньше вероятность возникновения ошибки второго рода.
Переменные потока и запасы
Все экономические переменные, которые имеют временное измерение, т.е. величины которых можно измерить по истечении времени называем переменными потока. А запас не имеет временное измерение.
Показатели вариации
Чтобы знать, насколько далеко значение совокупности простирается от центральной тенденции, вычисляют вариацию (на английском dispersion или variability, но не путайте с variation). Есть несколько показателей вариации. Это размах, межквартильный размах, среднее линейное отклонение, дисперсия и стандартное отклонение.
Типы выборки
Для расследования генеральной совокупности применяют два вида выборки. Случайную и неслучайную выборку. Простая, систематическая, стратифицированная и кластерная выборка являются случайными выборками. Стихийная, удобная и квотная выборка являются примером неслучайной выборки.
Скользящее среднее значение
Среди наиболее популярных технических индикаторов чаще всего, скользящее среднее значение используются для измерения направления текущего тренда. Самая простая формула скользящей средней, известна как Простое Скользящее Среднее значение.
Генеральная совокупность и выборка
Генеральной совокупностью называют всё исследуемое множество. На английском языке этот термин называется популяцией (population). Выборкой (на английском sample) называют некоторое случайно отобранное подмножество из генеральной совокупности.
Типы данных в статистике
Такие выражения, как минимум, максимум, медиана и процентиль имеют значение лишь для порядковых данных. Порядковые данные делятся на метрические и неметрические.
Что такое тренд?
Термины тренд и тенденция используются в различных целях. Люди часто говорят о тенденции относительно роста цен и падения курса какой-то валюты. Здесь мы раскроем статистическое значение этих терминов.
Ошибка репрезентативности
Стандартная ошибка (standard error) и ошибка репрезентативности часто употребляются, как взаимозаменяемые термины. Ошибка репрезентативности показывает, насколько результаты, полученные при выборочном наблюдении отличаются от результатов, полученных при исследовании генеральной совокупности.
Среднее значение, медиана и мода
Все чаще встречаем такие термины, как Бизнес-аналитика, Система поддержки принятия решений, Предсказательная аналитика. Но их уже достаточно распиарили и без нас. Поэтому остановимся на объяснении этих трех терминов: среднее значение, медиана и мода.
Гипотеза о равенстве генеральных дисперсий двух нормальных распределений
Две средние мы , очередь за дисперсиями. Из двух нормальных ген. совокупностей извлечены независимые выборки объёмом и и найдены их исправленные дисперсии: и соответственно. Совершенно понятно, что эти значения случайны и отличны друг от друга. Но возникает вопрос: значимо или незначимо это отличие? Для ответа на этот вопрос на уровне значимости проверяется гипотеза о равенстве генеральных дисперсий . Если она будет принята, то различие между выборочными значениями объяснимо случайными факторами.
Для проверки этой гипотезы используют критерий , где – бОльшая исправленная дисперсия, а – мЕньшая.
Данная случайная величина имеет (так называемое F-распределение) со степенями свободы , если или , если . То есть, степень свободы соответствует выборке с бОльшей исправленной дисперсией.
В качестве альтернативы рассматривают одну из следующих гипотез:
1) (если ) либо (если ). Для этой гипотезы строят правостороннюю критическую область:
Критическое значение можно найти по таблице критических значений F-распределения, а ещё лучше – с помощью стандартной функции Экселя, используйте тот же Калькулятор (Пункт 12).
2) – для этой гипотезы строится двусторонняя критическая область:
Однако для решения нашей задачи достаточно найти лишь правое критическое значение .
Дело в том, что , и поэтому случайное значение (бОльшее единицы) заведомо не может попасть в левый кусок критической области.
Далее на основании выборочных данных рассчитывается наблюдаемое значение критерия , и если оно попадает в критическую область ( для обоих случаев), то гипотеза отвергается. Если , то принимается.
Рассматриваемая гипотеза часто возникает, когда требуется сравнить точность двух приборов, инструментов, станков, двух методов исследования. И сейчас мы разберём эту стандартную задачу:
Пример 47
Некоторая физическая величина измерена и раз двумя различными способами. По результатам измерений найдены соответствующие погрешности . Требуется на уровне значимости 0,05 проверить, одинаковую ли точность обеспечивают эти способы измерений.
Ситуации тут могут быть разные: это измерение двумя однотипными инструментами (например, двумя линейками), или инструментами разными (например, линейкой и штангенциркулем), или речь вообще идёт о двух методах измерения (например, с зажмуренным левым и правым глазом).
И возникает вопрос: различие между случайно или обусловлено тем, что какой-то способ точнее?
Решение: полагая, что погрешности измерений распределены нормально, проверим гипотезу о том, что точность двух способов одинакова против конкурирующей гипотезы (она правдоподобнее, нежели ).
Для проверки гипотезы используем критерий , где – бОльшая исправленная дисперсия, а – мЕньшая.
Найдём критическое значение . Степень свободы должна соответствовать выборке с бОльшей дисперсией, следовательно, и . По соответствующей таблице либо с помощью Калькулятора (Пункт 12) находим:
При нулевая гипотеза принимается, а при (в критической области) – отвергается.
Вычислим наблюдаемое значение критерия:, поэтому на уровне значимости 0,05 нет оснований отвергать гипотезу . Иными словами, различие выборочных значений обусловлено случайными факторами, но прежде всего, малым количеством опытов.
Так, если бы было проведено в 10 раз больше измерений и получены те же самые погрешности, то , и гипотеза о равенстве ген. дисперсий уже отвергается. То есть здесь расхождение между уже нельзя объяснить случайностью, а объяснимо оно именно тем, что второй способ менее точный (справедлива гипотеза ).
Ответ: на уровне значимости 0,05 точность способов измерения одинакова.
Творческая задача для самостоятельного решения, случай из жизни:
Пример 48
Две группы студентов-первокурсников написали контрольную по математическому анализу со следующими результатами: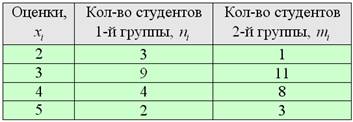
Предполагая, что успеваемость студентов распределена нормально, на уровне значимости 0,1:
1) Проверить гипотезу – о том, что группы однородны по составу (в плане соотношения лучше и хуже успевающих студентов) против конкурирующей гипотезы ,
и в случае однородности групп :
2) Проверить гипотезу – об одинаковой успеваемости групп против гипотезы о том, что одна из групп более слабая.
Вспоминаем, что такое дискретный вариационный ряд и как рассчитываются его характеристики. Не позволяй душе лениться! – в жизни пригодится, все числа уже в Экселе.
Ну что, порешаем ещё задачки? …конечно, порешаем! – ведь я маньяк в лучшем смысле этого слова:
Гипотеза о равенстве коэффициента уравнения нулю
77-1. Как проверить гипотезу о нулевом значении теоретического коэффициента регрессии?
Для проверки нулевой гипотезы H0 о равенстве нулю некоторого коэффициента регрессионного уравнения (H0:β2=0, H: β2≠0) необходимо сравнить фактическое значение статистики, найденное по формуле с критическим значением t-статистики Стьюдента для выбранного уровня значимости, то есть со значением двусторонней (1-α) квантили t-статистики Стьюдента с n-k степенями свободы. Величина α характеризует допустимый уровень вероятности ошибиться, отвергнув нулевую гипотезу, когда она верна.
Если фактическое значение t-статистики Стьюдента больше критического значения статистики, то нулевая гипотеза отвергается для данного уровня значимости α, иначе нулевая гипотеза не может быть отвергнута для данного уровня значимости α. В случае отвержения нулевой гипотезы для уровня значимости говорят, что коэффициент β регрессионного уравнения значим на уровне значимости α (или, говорят, что оценка коэффициента β значимо отличается от нуля), и соответствующий ему регрессор объясняет вариацию зависимой переменной. В противном случае говорят, что коэффициент незначим на уровне значимости α.
Второй способ проверки гипотезы – сравнить p-значение (фактическую вероятность принятия нулевой гипотезы данного коэффициента регрессии) с выбранным уровнем значимости. Если выполняется условие p |t критич|, то гипотеза H0 отвергается, если меньше, то подтверждается
79. Что такое p-значение (p-value, обозначаемое в программе EViews как Prob.) для
статистического критерия?
Метод p-value («метод значения вероятность») p-value = Prob – вероятность того, что случайно будет получен результат лучше, чем у нас (тот, что рассчитан). Если p-value маленький, то это хорошо, а если большой, то плохо.
80. В чем заключается техника работы с p-значением при проверке гипотез?
Смотрим значение prob. в таблице с результатами регрессии и сравниваем с 0,01 и 0,05.
Иначе коэффициент (уравнение) не значим.
81. Как рассчитать p-значение в случае, если невозможно получить доступ к эконометрической программе, или в ней не предусмотрен его расчет?
Открываем таблицу t-распределения, смотрим ряд для нашего числа степеней свободы. Если в нем есть значение t-статистики для рассматриваемого параметра, то уровень значимости (верх таблицы) будет как раз искомым значением p. Если значение t-статистики располагается между двумя табличными, то на основе значений для двух табличных можно приближенно рассчитать искомое по формуле , где t – значение t-статистики, t1 – первое из табличных значений, t2 – второе (большее, правее первого в ряду), а p1 и p2 – значения p соответственно для первого и второго табличных значений t-статистики.
82. Что такое ошибки первого и второго рода в проверке гипотез о коэффициентах регрессии?
Ошибка I рода состоит в том, что мы отвергаем Н0, когда на самом деле она истина.
Ошибка II рода имеет место в случае, если мы принимаем Н0, когда она ложна.
83. Какова связь ошибок первого и второго рода при проверке гипотез о коэффициентах регрессии?
При уменьшении вероятности ошибки 1ого рода увеличивается вероятность ошибки 2ого рода.
84. Что такое мощность критерия?
Мощность критерия (теста)- это вероятность допустить ошибку II рода (β), то есть принять ложную гипотезу. Вычисляется по формуле (1 − β). Таким образом, чем выше мощность, тем меньше вероятность совершить ошибку второго рода. Используя односторонний критерий вместо двустороннего, можно получить большую мощность при любом уровне значимости. Нужно, однако, помнить, что выигрыш в мощности будет получен только в условиях, когда использование одностороннего критерия оправдано.
4.2 Общие принципы проверки статистических гипотез
Процедура проверки нулевой гипотезы в
общем случае включает следующие этапы:
1.задается допустимая вероятность ошибки
первого рода (Ркр=0,05)
2.выбирается статистика критерия (Т)
3.ищется область допустимых значений
4.по исходным данным вычисляется
значение статистики Т
5. если Т
(статистика критерия) принадлежит
области принятия нулевой гипотезы, то
нулевая гипотеза принимается (корректнее
говоря, делается заключение, что исходные
данные не противоречат нулевой гипотезе), а
в противном случае нулевая гипотеза
отвергается и принимается альтернативная
гипотеза.
Это основной принцип проверки всех
статистических гипотез.
Обычно первые три этапа
выполняют профессиональные математики, а
последние два – пользователи для своих
частных данных.
В современных
статистических пакетах на ЭВМ используются
не стандартные уровни значимости, а уровни,
подсчитываемые непосредственно в процессе
работы с соответствующим статистическим
методом. Эти уровни, обозначенные буквой P, могут
иметь различное числовое выражение в
интервале от 0 до 1, например, 0,7 0,23 0,012.
Понятно, что в первых двух случаях
полученные уровни значимости слишком
велики и говорить о том, что результат
значим нельзя. В последнем случае
результаты значимы на уровне 12 тысячных.
Это достоверный результат.
При
проверке статистических гипотез с помощью
статистических пакетов, программа выводит
на экран вычисленное значение уровня
значимости Р и подсказку о возможности
принятия или неприятия нулевой гипотезы.
Если
вычисленное значение Р
превосходит выбранный уровень Ркр,то принимается нулевая гипотеза, а в
противном случае — альтернативная
гипотеза. Чем меньше вычисленное значение Р,
тем более исходные данные противоречат
нулевой гипотезе.
Число
степеней свободы у какого-либо
параметра определяют как число опытов, по
которым рассчитан данный параметр, минус
количество одинаковых значений, найденных
по этим опытам независимо друг от друга.
Величина Ф называется мощностью
критерия и представляет собой вероятность
отклонения неверной нулевой гипотезы, то
есть вероятность правильного решения. Мощность
критерия – вероятность попадания
критерия в критическую область при условии,
что справедлива альтернативная гипотеза.
Чем больше Ф, тем вероятность ошибки 2-го
рода меньше.
Пример ошибок двух типов
Со сложными понятиями легче разобраться на примере.
Во время производства некоего лекарства от учёных требуется чрезвычайная осторожность, так как превышение дозы одного из компонентов провоцирует высокий уровень токсичности готового препарата, от которого пациенты, принимающие его, могут умереть. Однако на химическом уровне выявить передозировку невозможно.
Из-за этого перед тем как выпустить лекарство в продажу, небольшую его дозу проверяют на крысах или кроликах, вводя им препарат
Если большая часть испытуемых умирает, то лекарство в продажу не допускается, если подопытные живы, то лекарство разрешают продавать в аптеках.
 Первый случай: на самом деле лекарство было не токсично, но во время эксперимента была допущена оплошность и препарат классифицировали как токсичный и не допустили в продажу. А=1.
Первый случай: на самом деле лекарство было не токсично, но во время эксперимента была допущена оплошность и препарат классифицировали как токсичный и не допустили в продажу. А=1.
Второй случай: в ходе другого эксперимента при проверке другой партии лекарства решено, что препарат не токсичен, и в продажу его допустили, хотя на самом деле препарат был ядовит. А=2.
Первый вариант повлечёт за собой крупные финансовые затраты поставщика-предпринимателя, так как придётся уничтожить всю партию лекарства и начинать с нуля.
Вторая ситуация спровоцирует смерть пациентов, купивших и употреблявших это лекарство.
Проверка гипотез для инвестиций
В качестве примера, связанного с финансовыми рынками, предположим, что Алиса видит, что ее инвестиционная стратегия дает более высокий средний доход, чем простая покупка и удержание акций. Нулевая гипотеза утверждает, что между двумя средними доходами нет разницы, и Алиса склонна верить в это до тех пор, пока не сможет прийти к противоречивым результатам.
Для опровержения нулевой гипотезы потребуется показать статистическую значимость, которую можно найти с помощью различных тестов. Альтернативная гипотеза будет утверждать, что инвестиционная стратегия имеет более высокий средний доход, чем традиционная стратегия «купи и держи».
Одним из инструментов, который можно использовать для определения статистической значимости результатов, является значение p. Значение p представляет собой вероятность того, что разница, такая большая или большая, чем наблюдаемая разница между двумя средними доходами, может возникнуть исключительно случайно.
Значение p, меньшее или равное 0,05, часто используется, чтобы указать, есть ли доказательства против нулевой гипотезы. Если Алиса проведет один из этих тестов, например, тест с использованием нормальной модели, в результате чего получится значительная разница между ее доходностью и доходностью покупки и удержания (значение p меньше или равно 0,05), тогда она сможет отклонить нулевую гипотезу и заключить альтернативную гипотезу.