Кто изобрёл механические калькуляторы подобного рода, и когда они появились?
- По версии немцев этим человеком был их соотечественник, Карл Кубер (основоположник компании Addiator), в 30-х годах XX века.
- По их же версии, в основу аналогичного механического калькулятора, разработанного русскими инженерами (был выпущен в 1967 году к 50-летию Советского Союза), легли чертежи одной из машинок Additor’а, которые вошли в список трофеев, увезённых русскими из Германии после их победы во Второй мировой войне.
- По версии французов, первый механический калькулятор подобного рода был изобретён их соотечественником. Французом по фамилии Тронсет. В 1889 году.
- Однако, также существует версия, что «изобретение» Тронсета было переделкой гораздо более раннего прототипа, изготовленного в 1720 году. Так что похоже Sub-Zero уходит корнями в 18-й век.
Вот такая удивительная изящная машинка из древнего технического прошлого. Коллеги, а у кого-нибудь Sub-Zero в хозяйстве водится? Или может быть аналогичная машинка? Поделитесь пожалуйста впечатлениями и примите участие в опросе.
О важности использования счетов
Не так давно инструкция как считать на деревянных счетах была в каждом магазине, бухгалтерии, на складах. В СССР и других странах в прошлом веке активно пользовались таким инструментом, потому что при больших объемах работы это надежнее, чем полагаться на умственный счет без записи.
На какое-то время абакусы пропали из школ и с предприятий, но по мере распространения популярности ментальной арифметики стали стремительно возвращаться в учебные центры. Они используются при обучении детей математике, потому что помогают понять сам принцип счета, значение основных действий – сложения, вычитания, умножения и деления.
В продаже вы найдете модели, которые отличаются по основным параметрам:
- Количество костяшек и спиц.
- Наличие выделенного пространства для «пятерок».
- Материал изготовления.
- Вес и размеры.
Ребенку для занятий лучше купить крупный абакус, на котором будет удобно передвигать костяшки даже тем, у кого мелкая моторика пока недостаточно хорошо развита.
Как набирать числа на деревянных счетах
Как мы уже говорили, каждая спица – это разряд. Потому чтобы собрать какое-либо число, нужно передвинуть определенное количество костяшек. К примеру, нам нужно набрать число 125. Для этого передвигаем одну сотню, два десятки и пятерку (либо пять косточек по единице).
Этот принцип важно освоить, потому что на нем будет строиться выполнение различных математических действий. Именно когда мы начинаем решать примеры при помощи абакуса, можно говорить, что мы используем счеты и считаем на них
Как складывать на деревянных счетах
Сложение обычно становится первой операцией, которую начинают изучать на регулярных занятиях ментальной арифметикой.
Начинаем всегда с двух чисел, берем не слишком большие. Если вы работаете с простыми числами, можно не думать про разряды на абакусе. К примеру, нужно сложить 2 и 5. Дайте ребенку передвинуть две костяшки на одной спице и пять на другой. Остается только пересчитать, сколько косточек было передвинуто и ответ готов.
Разряды можно начинать использовать в том случае, если мы работаем с двух-, трехзначными и более крупными числами. Именно так ребенок начнет понимать сами принципы использования математики.
Как вычитать на деревянных счетах
Вычитание работает по обратному принципу. Для этого нужно сначала установить нужное количество костяшек, а потом вычесть из большего числа меньшее. Соответственно, мы просто убираем достаточное количество косточек и пересчитываем остаток.
Как умножать на деревянных счетах
Когда мы уже освоили сложение и вычитание, можно переходить к более сложным действиям. Предполагается, что к моменту начала занятий ребенок уже должен знать таблицу умножения и понимать общие принципы выполнения таких действий.
Главное правило умножения – движение от большего к меньшему. При этом, нужно раскладывать числа, с которыми мы работаем, на составляющие. Представим, что нужно умножить 11х9. Для этого потребуется разделить первое число на десятки и единицы, а потом умножить все это на второе. Выглядеть процесс будет следующим образом:
- 10х9 = 90
- 1х9 = 9.
Далее складываем полученное. 90+9 = 99. Это и будет наш ответ. Но как отобразить его на абакусе? Нужно просто переместить 6 костяшек в разряде единиц и 6 в разряде десяток.
Как делить на деревянных счетах
Процесс деления стоит начинать изучать позже всего, потому что многие отмечают его сложность. Как известно, любой подобный пример состоит из трех частей – делимое, делитель и частное (результат).
На абакусе лучше всего отвести левую сторону под делимое, правую под делитель и между ними оставить пространство для высчитывания частного. Процесс будет во многом напоминать умножение, но там где мы использовали сложение, придется вычитать.
Как пользоваться утилитой Dram Calculator for Ryzen
Предлагаем вашему вниманию подробную инструкцию, позволяющую быстро освоить и настроить программу для получения максимальной скорости работы памяти (к сожалению, сайт разработчика не русифицирован).
Интерфейс программы
Итак, программа успешно установлена. Кликаем по её значку и получаем следующее окно:
В верхней части утилиты расположено меню.
Ниже – таблица, состоящая из полей, в которые вносятся исходные данные, и полей вывода расчётных количественных показателей, которые нужно будет перенести в BIOS посредством ручного ввода.
Внизу расположены кнопки, с помощью которых запускается расчёт требуемого режима разгона памяти.
Заполнение данных
Откуда брать исходные данные? Лучший способ их получения – использование другой утилиты, Thaiphoon Burner. Её нужно скачать на официальном сайте (www.softnology.biz), инсталлировать и запустить.
После появления заставки находим в главном меню кнопку Read и кликаем по ней.
Появится окошко с параметрами установленного в вашем компьютере чипа оперативной памяти (производитель, версия ОЗУ её оценка).
Так, производитель указывается в поле Manufacturer, версия – в поле Part Number, оценка – в поле Die Density.
Все эти данные нужно перенести в утилиту Ryzen Dram Calculator:
- в поле Proccessor выбираем значение Ryzen 1 gen для чипа Ryzen 1000, или Ryzen + gen для чипа следующего поколения, Ryzen 2000;
- в поле Memory type нужно вставить значение, полученное в утилите Thaiphoon Burner (производитель памяти и её версия);
- в полк Profile version заносим версию профиля XMR из BIOS, именно оттуда программа при расчёте подгрузит недостающие параметры;
- в поле Memory rank необходимо указать ранг планки памяти. В большинстве случаев указываем единичку (одноранговая ОЗУ);
- в поле Frequency вводим ту частоту, до которой мы намереваемся разогнать память нашего компьютера;
- в поле BCLK необходимо указать базовую частоту Motherboard (по умолчанию – 100 МГц, если вы не её разгоняли, оставляем как есть);
- в поле DIMM Modules указываем число планок ОЗУ.
Получаем примерно следующий результат:
Загрузка данных из профиля BIOS XMP
Чтобы заполнить недостающие данные, заходить в BIOS не обязательно. Они будут подгружены автоматически после нажатия кнопки R-XMP:
Расчёт параметров разгона
Когда все исходные данные введены, можно приступать к расчёту параметров, которые необходимы для оверклокинга памяти вашего компьютера. Для этого нужно нажать на любую из трёх кнопок Calculate.
Полученные результаты для трёх режимов разгона ОЗУ будут отличаться только напряжением
Вам останется сделать скриншоты и перенести расчётные данные в BIOS, при этом особое внимание следует уделить заполнению таймингов и параметров напряжения (самих планок и чипсета)
Расчёт дополнительных параметров напряжения
Достаточно указания расчётных параметров в BIOS, рассчитанных в Ryzen Dram Calculator, для обеспечения стабильной работы памяти с более высокими скоростями. Но бывают случаи, когда у вас установлено нестандартное ОЗУ или вы хотите разогнать память до максимальных частот. Тогда вам придётся поменять ещё парочку параметров, получить которые можно во вкладке Advanced:
Это следующие параметры:
- VTT DDR Voltage – характеристика, от которой зависит стабильность функционирования шины ОЗУ;
- VDDP Voltage – параметр, определяющий стабилизировать функционирования самой памяти;
- VPP Voltage – рекомендуемое, минимальное и максимальное напряжение шины.
СОВЕТ. Прибегайте к этому способу только в крайнем случае, когда стандартных настроек оказалось недостаточно для разгона. Поскольку для каждого из параметров указывается не конкретное значение, а диапазон, подбирать оптимальные придётся экспериментальным путём.
Дополнительные калькуляторы
Наконец, используя вкладку Additional Calculators в верхнем меню утилиты, можно попробовать получить расчетные данные VTT DDR Voltage, указав напряжения планок ОЗУ в поле Dram Voltage:
Проблема нуля на счетах
При вычислении задач с тремя цифрами в уравнении, где ноль является частью двузначного числа, например 80, 90, 40 и т. Д., Мы по-прежнему считаем до четвертой строки, чтобы установить второе число. Например, 50 x 9 потребует такой же процедуры.
Давай попробуем.
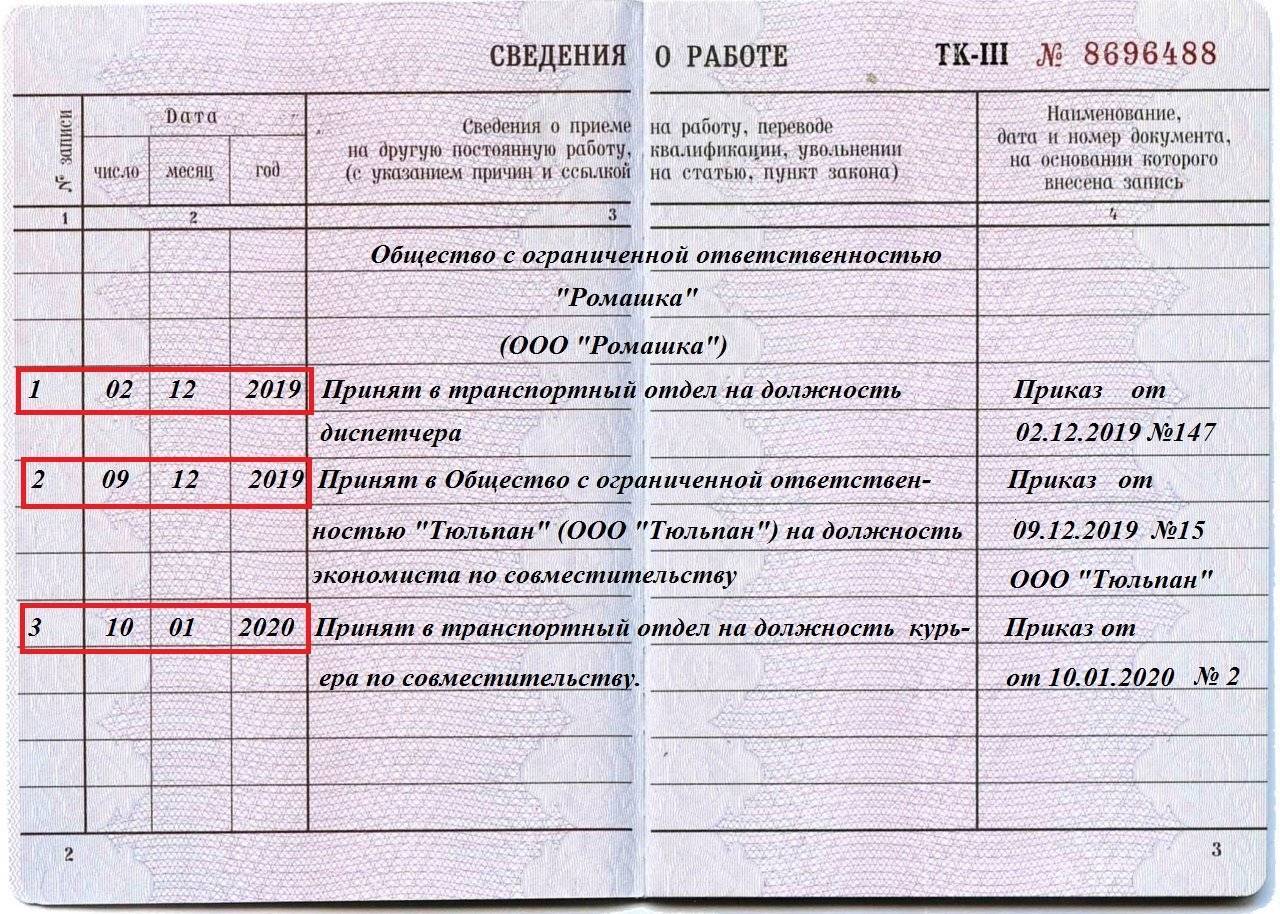
Поместите 9 в крайний левый ряд. Теперь поместите 50 в четвертый ряд справа. Задача должна быть настроена как на фото. Умножить: 9 х 50. Ответ будет: 450, которые вы поместите на третий, второй и первый ряды бусинок с правой стороны. После очистки 9 и 50 ответ должен выглядеть как на фото. Это основные шаги для работы с уравнениями, состоящими из трех цифр, в задаче умножения на счетах. Теперь, когда работа сделана, счеты абакуса можно остановить. Другая проблема с нулем возникает, когда конечный продукт меньше 100. В этих случаях мы считаем сотни за ноль. Например: 9 x 11 будет считаться таким образом: (0) сотни, 9 десятков и 9 единиц. 3 x 12 будут посчитаны таким образом: (0) сотни, 3 десятки и 6 единиц. Наслаждайтесь счетами абакуса, и вы можете стать экспертом в использовании счетного инструмента в будущем.
На счетах «450».
ЧТО ЕЩЕ ПОЧИТАТЬ
Как считать на абакусе! Решение на счётах в одной статье Ментальная Арифметика Онлайн Тренажер Бесплатно Как быстро и легко в игровой форме выучить таблицу умножения КАК РЕШАТЬ ЗАДАЧИ
Простота арабских цифр
Мы привыкли к тому, что цифры 1,2, 3 и т.д., которыми мы пользуемся ежедневно, называются арабскими и придумали их арабы. На самом деле эти цифра возникли в Индии примерно в IV—V вв. Просто арабы принесли оттуда эту форму записи чисел, которая потом распространилась через Северную Африку, Испанию и в X в. попала в Европу.
Преимущество арабских цифр по сравнению с римскими не в их написании, а в гениальном изобретении, при котором «вес» цифры определяется ее положением. Так, например, 3 в числе 23 «весит» всего три единицы, а уже в числе 232 — три десятка единиц. Представьте, какие бы сложные вычисления нам пришлось производить, если бы до сих пор пользовались римскими числами. Чтобы понять это, попробуйте, например, перемножить XVII на СХХIII (17 на 123).
Как работать на счетах
Для того чтобы набрать на счетах необходимое вам число, понадобятся костяшки, которые будут соответствовать нужному классу цифр. Их необходимо передвигать справа на лево. Чтобы вам было проще разобраться, можно рассмотреть все это на наглядном примере. Так, представьте, что вам нужно набрать 4 733,64. Для этого сначала передвиньте в верхнего ряда 4 костяшки, которые будут означать 4 тысячи. После этого на втором ряду отсчитайте 7 костяшек, что будет равносильно 7 сотням. На третьем ряду отсчитайте 3 костяшки, т.е. десятки. С четвертого ряда передвиньте 3 единицы. Дальше также нужно убрать 6 десятых и 4 сотых.
Если у вас уже есть счеты, попробуйте применить этот метод подсчета на практике. Так вы сможете быстрее освоить эту науку. На самом деле разобраться в этом не сложно. Нужно лишь попрактиковаться.
Умножение на счетах
Несмотря на то, что умножение на счетах считается одним из сложных действий, освоить его выполнение вполне возможно. Если вы только учитесь этому, то лучше начинать осваивать небольшие значения. Можно рассмотреть несколько несложных вариантов умножения.
Для умножения какого-либо числа на два нужно просто набрать его на счетах, а затем прибавить еще одно такое же число. Если нужно умножить число на три, следует прибавить число еще раз. Чтобы легче было произвести умножение на 4, нужно сначала умножить число на 2, как было описано ранее, а затем снова умножить на 2. Если вы хотите умножить число на 5, то для этого сначала разделите его на 2, а потом умножьте на 10. Это уже не сложно, нужно лишь передвинуть костяшки на уровень выше. Это лишь некоторые операции на умножение, которые вы сможете научиться выполнять на начальном этапе.
Как считать умножение на абакусе
Изучая счеты, мы замечаем, что имеется не менее тринадцати рядов бусинок. Чтобы произвести умножение, мы должны мысленно представить счеты как разделенные посередине этих рядов, примерно в седьмом ряду бусинок. Это потому, что мы разместим одно число слева от счетчика, а другое — справа.
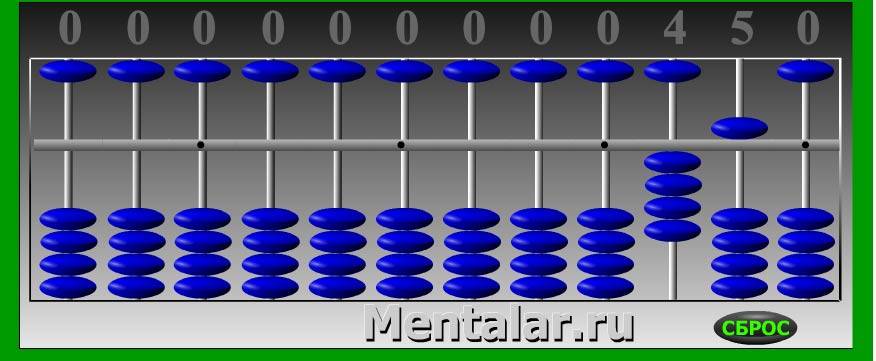
Давайте начнем. Поместите 25 x 7 на счеты. Поместите 25 в самые дальние ряды бусинок. Теперь давайте разместим цифру 7. Для этого мы знаем, что в задаче умножения есть три цифры: 2, 5 и 7. Для умножения нужно дать дополнительный ряд бусинок «для счётов». По сути, мы думаем: три цифры в уравнении плюс ряд бусинок «для счётов». Это означает, что цифра 7 будет размещена в четвертом ряду справа
Важность этого действия заключается в том, что он дает пользователю счетного инструмента некоторое указание на то, что ответ будет в сотнях, оставшиеся три строки справа. Задача должна быть настроена как на фото
Счет «25 X 7».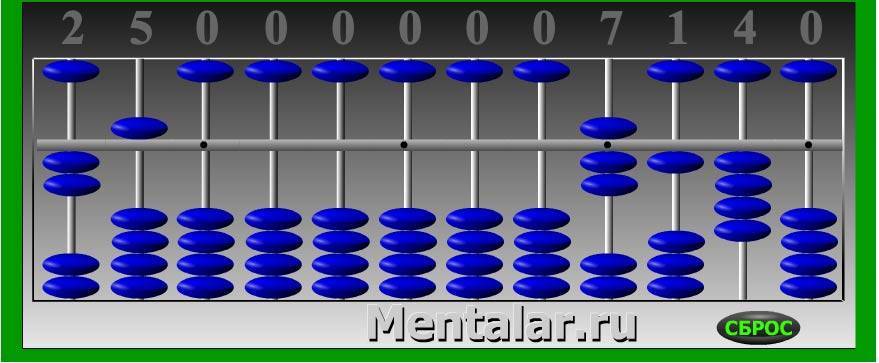
Здесь счет показывает как «7 умножить на два десятка».
Коммерческий успех и долгая жизнь
Производство счетных машин длительное время оставалось делом невыгодным. Лишь в 1820 г. французскому предпринимателю Шарлю-Ксавье Тома де Колмару (1785—1870) удалось создать первый механический счетный прибор, принесший своему изобретателю коммерческий успех.
В своей машине Колмар использовал принцип построения счетного механизма Лейбница, что позволяло быстро производить основные математические операции. Получив патент на свою машину, изобретатель запустил ее в массовое производство. Достаточно быстро она завоевала звание самой надежной счетной машины и не случайно занимала достойное место на столах счетоводов Европы. Кроме того, этот вычислитель поставил своеобразный мировой рекорд по продолжительности продаж: последняя модель была продана в начале XX в.
Режимы работы математического калькулятора
Простой онлайн калькулятор математический и карманный, легко помещается в мобильный телефон и позволяет выполнять простые арифметические действия, например, когда необходимо сложить, вычесть, умножить или разделить положительные и отрицательные числа. Это первый и незаменимый помощник дома, может помочь в дороге и на учебе, он полностью заменяет обычные механические машины, которые не всегда под рукой.
Калькулятор способен на многое, нет необходимости устанавливать на ваш смартфон или планшет, доступен на сайте с компьютера и можно пользоваться с другим набором калькуляторов.
Функции и команды кнопок
Онлайн-калькулятор позволяет бесплатно и точно вычислить и решить бухгалтерские данные. Например, он легко заменит конвертер валют, если знать актуальный курс. Им удобно посчитать бытовые задачи и использовать на любом устройстве, размеры легко адаптируются под нужный экран. Без использования другой научной вычислительной техники.
Назначение кнопок
Имеет возможность решения выражений и сложных задач не всегда требуется специальное обучение, счеты или инженерный калькулятор. Часто достаточно подробно ознакомиться с количеством и описанием значения каждой кнопки, ввести ввод клавиатуры и произвести точный расчет просто:
Клавиши цифр
7
8
9
4
5
6
1
2
3
00
Умножения чисел
×
Деления чисел
Сложение
+
Вычитание
–
Вывод результата
=
Удаление последнего знака
←
Изменение математического знака на противоположный
+/-
Квадратный корень
√
Отделение дробной части в десятичную
,
Операция с наценкой
MU
Сохранение результата в памяти со знаком
M+
Сохранение результата в памяти со знаком
M-
Демонстрация памяти на дисплее
MR
Сброс содержимого памяти
MC
Сброс значений и параметров памяти
AC
Сброс значений и сохранение содержимого памяти
C
Примеры вычислений расчета на калькуляторе
Калькулятор позволяет выполнять не только вычисления с двузначными, трёхзначными (и более) числами, но и поддерживает решение более сложных задач: расчет процентов, вычисление квадратных корней, возведение в степень. Одна из самых востребованных функций: определение сколько процентов составляет часть от числа и вычитания. Рассмотрим несколько методов работы и примеров:
Умножение:
11×24=264
11
×
24
=
Вычитание:
7-4=3
7
–
4
=
Деление:
88÷4=22
88
÷
24
=
Квадратный корень:
64√=8
64
√
=
Сложение:
20%+150=180
150
+
20%
=
Какая у Sub-Zero начинка?
Sub-Zero состоит из трёх компонентов: 1) цельный металлический корпус с шестью подвижными зубчатыми полосками внутри; 2) карандаш, при помощи которого задаются числовые значения; 3) рукоятка для сброса регистров в 0.
- На корпусе Sub-Zero нарисованы цифры и предусмотрены отверстия для доступа к шести зубчатым металлическим полоскам и для просмотра содержимого двух регистров.
- Шесть зубчатых металлических полосок – это подвижные механические элементы калькулятора. На этих полосках нарисованы цифры. Посредством них задаются значения регистров и выполняются арифметические операции сложения и вычитания.
- В середине корпуса и у его основания расположены два набора из шести отверстий, через которые видны цифры, нанесённые на зубчатые полоски. В верхнем регистре (т.е. в том, что посередине) отображаются положительные значения, в нижнем – отрицательные.
- Верхняя часть калькулятора используется для сложения, а нижняя – для вычитания. Иногда в одном из регистров отображается стрелка. Это означает, что ответ нужно смотреть в другом регистре.
Устройство для умножения и деления
В 1673 г. немецкий математик и философ Готфрид Вильгельм Лейбниц (1646—1716) создал механическое счетное устройство, которое не только складывало и вычитало, но умножало и делило 12-разрядные числа. В основе механизма лежал изобретенный Лейбницем ступенчатый валик, представлявший собой цилиндр с нанесенными на нем зубцами различной длины. Ускорить повторяющиеся операции сложения позволяла специальная рукоятка, с помощью которой пользователь вращал цилиндр.
Готфрид Вильгельм Лейбниц (1646—1716)
По некоторым данным один экземпляр счетной машины Лейбница был приобретен Петром I, который затем подарил его китайскому императору, желая удивить последнего европейскими техническими достижениями. Кстати, именно зубчатые колеса Лейбница в дальнейшем стали основой массовых счетных приборов — арифмометров, которыми широко пользовались вплоть до середины XX в.
Тригонометрический калькулятор онлайн — примеры
Как произвести онлайн расчет синусов и косинусов, тангенсов
Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами. 1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан. 1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан
1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.
Для включения того или иного режима измерения нажмите нужную кнопку:
где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.
В качестве самого простого примера найдем синус 90 градусов. Нажмите:
90
Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:
60
Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.
Для их ввода необходимо переключить интерфейс, нажав , появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.
Преобразование с кнопкой Dms и Deg на калькуляторе
позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. производит обратный перевод – в формат «градусы; минуты; секунды».
Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:
35,140453 35,23459166666666666666
Переведем в прежний формат: 35,23459166666666666666 35,140453
Десятичный логарифм онлайн
Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:
1
Получается 0 в итоге. Для подсчета lg100 нажмем так:
100
Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.
Так же вычисляется натуральный логарифм, но кнопкой .
Как пользоваться памятью на калькуляторе
Существующие кнопки памяти: M+, M-, MR, MS, MC.
Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.
MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.
Пример. Внесем сто сорок пять в память программы:
145
После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:
На экране отобразится снова 145.
Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем , либо для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой получится 230, а во втором, после нажатия и получится 60.
Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.
Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Из этой статьи вы узнаете, как пользоваться основными функциями научного (инженерного) калькулятора. Научный калькулятор пригодится при изучении алгебры, геометрии и тригонометрии.
Найдите основные функции. На калькуляторе есть несколько функций, которые понадобятся для решения алгебраических, тригонометрических, геометрических и других задач. Найдите на калькуляторе следующие функции:
О важности использования счетов
Не так давно инструкция как считать на деревянных счетах была в каждом магазине, бухгалтерии, на складах. В СССР и других странах в прошлом веке активно пользовались таким инструментом, потому что при больших объемах работы это надежнее, чем полагаться на умственный счет без записи.
На какое-то время абакусы пропали из школ и с предприятий, но по мере распространения популярности ментальной арифметики стали стремительно возвращаться в учебные центры. Они используются при обучении детей математике, потому что помогают понять сам принцип счета, значение основных действий – сложения, вычитания, умножения и деления.
В продаже вы найдете модели, которые отличаются по основным параметрам:
- Количество костяшек и спиц.
- Наличие выделенного пространства для «пятерок».
- Материал изготовления.
- Вес и размеры.
Ребенку для занятий лучше купить крупный абакус, на котором будет удобно передвигать костяшки даже тем, у кого мелкая моторика пока недостаточно хорошо развита.
Как набирать числа на деревянных счетах
Как мы уже говорили, каждая спица – это разряд. Потому чтобы собрать какое-либо число, нужно передвинуть определенное количество костяшек. К примеру, нам нужно набрать число 125. Для этого передвигаем одну сотню, два десятки и пятерку (либо пять косточек по единице).
Этот принцип важно освоить, потому что на нем будет строиться выполнение различных математических действий. Именно когда мы начинаем решать примеры при помощи абакуса, можно говорить, что мы используем счеты и считаем на них
Как складывать на деревянных счетах
Сложение обычно становится первой операцией, которую начинают изучать на регулярных занятиях ментальной арифметикой.
Начинаем всегда с двух чисел, берем не слишком большие. Если вы работаете с простыми числами, можно не думать про разряды на абакусе. К примеру, нужно сложить 2 и 5. Дайте ребенку передвинуть две костяшки на одной спице и пять на другой. Остается только пересчитать, сколько косточек было передвинуто и ответ готов.
Разряды можно начинать использовать в том случае, если мы работаем с двух-, трехзначными и более крупными числами. Именно так ребенок начнет понимать сами принципы использования математики.
Как вычитать на деревянных счетах
Вычитание работает по обратному принципу. Для этого нужно сначала установить нужное количество костяшек, а потом вычесть из большего числа меньшее. Соответственно, мы просто убираем достаточное количество косточек и пересчитываем остаток.
Как умножать на деревянных счетах
Когда мы уже освоили сложение и вычитание, можно переходить к более сложным действиям. Предполагается, что к моменту начала занятий ребенок уже должен знать таблицу умножения и понимать общие принципы выполнения таких действий.
Главное правило умножения – движение от большего к меньшему. При этом, нужно раскладывать числа, с которыми мы работаем, на составляющие. Представим, что нужно умножить 11х9. Для этого потребуется разделить первое число на десятки и единицы, а потом умножить все это на второе. Выглядеть процесс будет следующим образом:
- 10х9 = 90
- 1х9 = 9.
Далее складываем полученное. 90+9 = 99. Это и будет наш ответ. Но как отобразить его на абакусе? Нужно просто переместить 6 костяшек в разряде единиц и 6 в разряде десяток.
Как делить на деревянных счетах
Процесс деления стоит начинать изучать позже всего, потому что многие отмечают его сложность. Как известно, любой подобный пример состоит из трех частей – делимое, делитель и частное (результат).
На абакусе лучше всего отвести левую сторону под делимое, правую под делитель и между ними оставить пространство для высчитывания частного. Процесс будет во многом напоминать умножение, но там где мы использовали сложение, придется вычитать.
Инструкция на калькулятор (офисный)
ИНСТРУКЦИЯ НА КАЛЬКУЛЯТОР (офисный)
— выключение. Если в течение 8-11 мин. не нажималась ни одна клавиша, калькулятор автоматически отключается.
— арифметические операции
[CE/C] — сброс последнего набранного числа/сброс
— общий сброс
— занесение числа в память с плюсом
— занесение числа в память с минусом
— извлечение из памяти. После второго нажатия память обнуляется. В некоторых моделях данные функции разделены (клавиши )
— работа со второй ячейкой памяти
— операция «Повышение цены» (может не работать)
— автоматическое суммирование операций
— извлечение квадратного корня
— звуковое подтверждение нажатия клавиш вкл./выкл.
— стирание последней введенной цифры
A 0 2 3 F — переключатель положения знака
в десятичной дроби
0,2,3 — число знаков после запятой, А — режим расчета денежных единиц, F — фиксированная запятая
— переключатель режима округления
ИНСТРУКЦИЯ ПО ПРИМЕНЕНИЮ КАЛЬКУЛЯТОРА
Вычисление квадратного корня
/5 = 2.4
6 + 4 ´ 2 — 8 / 5 = 2.4
Вычисления с константами
4 ´ 3 =12, 4 ´ 5 = 20
6 / 2 = 3, 8 / 2 = 4
Вычисления с памятью
Питание от батареи G10*2
Примечание. В данной модели калькулятора возможно отсутствие, объединение или дополнение некоторых операционных клавиш.
Питание калькулятора — от источника питания 1.5 в типа G13.
Рабочая температура от 0 до +40оС
Средний срок эксплуатации — 5 лет.
Гарантия не распространяется на элементы питания.
Калькулятор не подлежит гарантийному ремонту, возврату или замене при отсутствии упаковки; при наличии механических повреждений.
Как работают счеты
Бухгалтерские деревянные счеты ушли в прошлое, и теперь мало кто понимает, как ими пользоваться. А ведь несколько десятков лет назад это был основной инструмент для проведения расчетов. В любом магазине продавец виртуозно управлялся с этим инструментом, а покупатели смотрели и даже тогда не понимали, как работают счеты. Со стороны расчеты выглядели волшебным действом, которым невозможно овладеть самостоятельно. Но теперь тайны исчезли, и вы сможете овладеть этим знанием.
Счеты устроены так:
- снизу находятся два ряда по десять костяшек: это десятые и сотые доли числа;
- дальше идет один ряд из четырех костяшек: это четверти;
- выше снова расположены несколько рядов по десять костяшек: это единицы, десятки, сотни, тысячи и т.д.
В середине каждого ряда находятся две темные костяшки. Это сделано для того, чтобы легче было отсчитать нужное количество. А в ряду, обозначающем тысячи, левая костяшка тоже темная.
Числовое значение каждого ряда.
По размеру счеты могут быть разными. Некоторые содержат 10 строк с костяшками, некоторые меньше. Но принцип работы на них всегда одинаков.
Считающие часы
Первый механический калькулятор, умевший выполнять различные арифметические действия, был построен немецким ученым Вильгельмом Шикардом (1592—1633) в 1623 г. Изобретатель назвал свою машину «Считающими часами». Вероятно, такое название она получила из-за того, что, как и в настоящих часах, работа ее механизма была основана на использовании звездочек и шестеренок.
Вильгельм Шикард (1592—1633)
«Считающие часы» Шикарда умели складывать и вычитать шестизначные числа и информировали пользователя о переполнении с помощью звонка. По некоторым данным, с помощью этого изобретения друг Шикарда, известный немецкий философ и астроном Иоганн Кеплер (1571—1630), рассчитывал сложнейшие астрономические таблицы.
К сожалению, сама машина и ее чертежи были потеряны в годы Второй мировой войны. Однако в 1960 г. группа энтузиастов построила точную копию этого вычислителя по обнаруженным древним записям и подтвердила его существование и работоспособность.
